SUMMARY
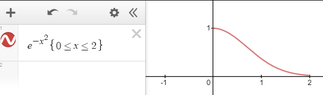
The discussion focuses on the function \( g(t) = e^{-t^2} \) and its properties regarding concavity and inflection points. It is established that \( g' > 0 \) for all \( x \in (0,2) \), indicating that \( g \) is increasing in this interval. Additionally, the second derivative \( g'' = e^{-x^2} > 0 \) confirms that \( g \) is concave up for \( x \in (0,2) \). The area accumulation function \( g'(x) = \int_0^x e^{-t^2} \, dt \) is also highlighted, showing the relationship between the function and its derivatives.
PREREQUISITES
- Understanding of calculus concepts, specifically derivatives and integrals
- Familiarity with the properties of exponential functions
- Knowledge of concavity and inflection points in graph analysis
- Ability to interpret area accumulation functions
NEXT STEPS
- Study the properties of exponential decay functions
- Learn about the Fundamental Theorem of Calculus
- Explore the concept of concavity and inflection points in detail
- Investigate the applications of area accumulation functions in real-world scenarios
USEFUL FOR
Students preparing for AP Calculus exams, educators teaching calculus concepts, and anyone interested in the analysis of exponential functions and their derivatives.