baseballfan_ny
- 92
- 23
- Homework Statement
- Get a 4th order taylor approximation for $$ f(p) = (1 + \frac {p^2} {m^2c^2})^{\frac 1 2} $$
- Relevant Equations
- $$\sum_{n=0}^\infty \frac {f^{(n)}(a) (x-a)^n} {n!}$$ around a = 0
So I just followed Taylor's formula and got the four derivatives at p = 0
##f^{(0)}(p) = (1 + \frac {p^2} {m^2c^2})^{\frac 1 2} ##
##f^{(0)}(0) = 1 ##
## f^{(1)}(p) = \frac {p} {m^2c^2}(1 + \frac {p^2} {m^2c^2})^{\frac {-1} 2} ##
## f^{(1)}(0) = 0 ##
## f^{(2)}(p) = \frac {1} {m^2c^2}(1 + \frac {p^2} {m^2c^2})^{\frac {-1} 2} - \frac {p^2} {m^4c^4}(1 + \frac {p^2} {m^2c^2})^{\frac {-3} 2} ##
## f^{(2)}(0) = \frac {1} {m^2c^2} ##
## f^{(3)}(p) = \frac {p} {m^4c^4}(1 + \frac {p^2} {m^2c^2})^{\frac {-3} 2} - \frac {3p^3} {m^6c^6}(1 + \frac {p^2} {m^2c^2})^{\frac {-5} 2} ##
## f^{(3)}(0) = 0##
## f^{(4)}(p) = \frac {1} {m^4c^4}(1 + \frac {p^2} {m^2c^2})^{\frac {-3} 2} +... ## (terms that are 0 when p = 0)
## f^{(4)}(0) = \frac {1} {m^4c^4} ##
Now that would give me $$ f(p) = 1 + \frac {p^2} {2! m^2c^2} + \frac {p^4} {4! m^4c^4} $$
$$ f(p) = 1 + \frac {p^2} {2m^2c^2} + \frac {p^4} {24m^4c^4} $$
But that's not right. The answer key has the following answer (and so does Wolfram) $$ f(p) = 1 + \frac {p^2} {2m^2c^2} - \frac {p^4} {8m^4c^4} $$
A picture of the answer key soln is below. Ignore the factor of ##Mc^2## outside the approximation.
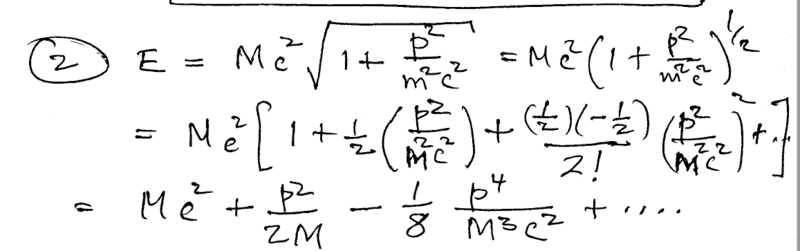
I noticed that the answer doesn't even get any of the derivatives equal to 0, and I was getting all the odd derivatives equal to 0. That makes me think I'm applying Taylor's formula incorrectly and it's more than just an algebra mistake?
##f^{(0)}(p) = (1 + \frac {p^2} {m^2c^2})^{\frac 1 2} ##
##f^{(0)}(0) = 1 ##
## f^{(1)}(p) = \frac {p} {m^2c^2}(1 + \frac {p^2} {m^2c^2})^{\frac {-1} 2} ##
## f^{(1)}(0) = 0 ##
## f^{(2)}(p) = \frac {1} {m^2c^2}(1 + \frac {p^2} {m^2c^2})^{\frac {-1} 2} - \frac {p^2} {m^4c^4}(1 + \frac {p^2} {m^2c^2})^{\frac {-3} 2} ##
## f^{(2)}(0) = \frac {1} {m^2c^2} ##
## f^{(3)}(p) = \frac {p} {m^4c^4}(1 + \frac {p^2} {m^2c^2})^{\frac {-3} 2} - \frac {3p^3} {m^6c^6}(1 + \frac {p^2} {m^2c^2})^{\frac {-5} 2} ##
## f^{(3)}(0) = 0##
## f^{(4)}(p) = \frac {1} {m^4c^4}(1 + \frac {p^2} {m^2c^2})^{\frac {-3} 2} +... ## (terms that are 0 when p = 0)
## f^{(4)}(0) = \frac {1} {m^4c^4} ##
Now that would give me $$ f(p) = 1 + \frac {p^2} {2! m^2c^2} + \frac {p^4} {4! m^4c^4} $$
$$ f(p) = 1 + \frac {p^2} {2m^2c^2} + \frac {p^4} {24m^4c^4} $$
But that's not right. The answer key has the following answer (and so does Wolfram) $$ f(p) = 1 + \frac {p^2} {2m^2c^2} - \frac {p^4} {8m^4c^4} $$
A picture of the answer key soln is below. Ignore the factor of ##Mc^2## outside the approximation.
I noticed that the answer doesn't even get any of the derivatives equal to 0, and I was getting all the odd derivatives equal to 0. That makes me think I'm applying Taylor's formula incorrectly and it's more than just an algebra mistake?