A cylinder has two sides containing gas and water separately

[highschoboy004]

Homework Statement

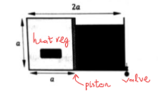
A rectangular cuboid is made up of two identical cubes which have side length a = 10 cm. The cubes are separated by a frictionless piston of negligible mass in the middle. The cube on the left contains gas which has initial temperature of 27 degree Celsius and initial pressure 4x10^5 N/m2. The cube on the right is full of water. We then open the valve to drain the water at a constant rate of 10cm3/s, if we are to keep the piston still then at what rate must we lower the gas temperature (°C/s)(using the heat regulator)?

Relevant Equations

nRT=pV

I think this problem is somehow weird since fluid has different pressures at different depths.

 

[haruspex]

I think this problem is somehow weird since fluid has different pressures at different depths.

You can assume the piston has some thickness so that it can’t rotate. So you only have to consider the net force each side. How it is distributed across the piston surface does not matter.

 

[highschoboy004]

You can assume the piston has some thickness so that it can’t rotate. So you only have to consider the net force each side. How it is distributed across the piston surface does not ma

Thanks a lot<3, I'm on my way with the numbers

 

[Lnewqban]

The cube on the right is full of water. We then open the valve to drain the water at a constant rate of 10cm3/s, if we are to keep the piston still then at what rate must we lower the gas temperature (°C/s)(using the heat regulator)?
Relevant Equations: nRT=pV

Welcome!

Another approach, which may bypass the weirdness of the problem regarding different pressures at different depths, is calculating the time for the water container to get empty.

The rate of cooling of the gas must be such that the physical volume that it occupies (under steady decreasing external force or pressure tending to zero) should remain constant at least within that period of time.

 

[highschoboy004]

Welcome!

Another approach, which may bypass the weirdness of the problem regarding different pressures at different depths, is calculating the time for the water container to get empty.

The rate of cooling of the gas must be such that the physical volume that it occupies (under steady decreasing external force or pressure tending to zero) should remain constant at least within that period of time.

Thanks, it does help a lot!!