A difficult boat and river problem

[Swap]

Homework Statement

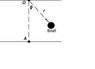
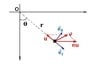
A boat is rowed with constant speed u starting from a point A on
the bank of a river of width d , which flows with a constant speed
nu . The boatman always points the boat at a point O on the other
side of the bank opposite to A. Find the equation of the path
r = f (theta ) for the boat.

Homework Equations

dx/dt = v

The Attempt at a Solution

I was able to find dr/dt in terms of theta. here is my expression dr/dt= u(1-nsin(theta)). The problem is when I integrate it i have to express dt in terms of d(theta) which I cannot find.

 

[hikaru1221]

I don't understand the problem much. Is it the boat's velocity relative to the ground, or its velocity relative to the water, which always points towards the water? I guess it's the latter, because if n>1 then there is no chance that the boatman can guide the boat towards O.

Let's assume so. I think your equation is a little bit incorrect (just a little bit, most is fine). First, you should write down the formula of velocity in polar coordinates, i.e. write down $$\vec{v}$$ in term of $$r$$ , $$\theta$$ and the unit vectors $$\vec{e}_r$$ and $$\vec{e}_{\theta}$$. Then use the condition that $$\vec{v}$$ is the sum of 2 velocity: u in the direction towards O and nu in the direction to the left. You should arrive at these 2 equations:

$$nusin\theta-u=\frac{dr}{dt}$$

$$nucos\theta=r\frac{d\theta}{dt}$$

From here, you can solve for $$r(\theta)$$.

 

[Swap]

can u explain me how u arrive at the second equation. I don't understand it

 

[hikaru1221]

Can you do step 1, i.e. writing down the formula of velocity in polar coordinates?

 

[Swap]

oh ok I got it. I didnt think of v=r(omega). Thx...