- #1
jonathanlv7
- 26
- 1
The problem is:
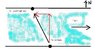
A 230-m-wide river has a uniform flow speed of 1.4 m/s through a jungle and toward the east. An explorer wishes to leave a small clearing on the south bank and cross the river in a powerboat that moves at a constant speed of 4.6 m/s with respect to the water. There is a clearing on the north bank 63 m upstream from a point directly opposite the clearing on the south bank. (a) At what angle, measured relative to the direction of flow of the river, must the boat be pointed in order to travel in a straight line and land in the clearing on the north bank? (b) How long will the boat take to cross the river and land in the clearing?
What I have been trying is, multiplying 4.6 by the costheta and sintheta (theta being the angle the boats velocity points toward from west towards north) to get the components of the velocity and then subtracting 1.4 from the x component because of the rivers current. Then I get position information by integrating the velocity equations. I set the x component of the position equal to -63 (I made west positive and east negative) and then solve for t. Then I plug that t into the y component of the position and try to solve for theta. I end up with 230costheta+63sintheta=70. I tried to solve it and quickly realized it is pretty much impossible to find theta from that. So if somebody could figure out what I need to change in how I'm trying to do this problem that would be great, I have been stuck on this problem for 3 days. Last problem in my homework set. Thank you!
A 230-m-wide river has a uniform flow speed of 1.4 m/s through a jungle and toward the east. An explorer wishes to leave a small clearing on the south bank and cross the river in a powerboat that moves at a constant speed of 4.6 m/s with respect to the water. There is a clearing on the north bank 63 m upstream from a point directly opposite the clearing on the south bank. (a) At what angle, measured relative to the direction of flow of the river, must the boat be pointed in order to travel in a straight line and land in the clearing on the north bank? (b) How long will the boat take to cross the river and land in the clearing?
What I have been trying is, multiplying 4.6 by the costheta and sintheta (theta being the angle the boats velocity points toward from west towards north) to get the components of the velocity and then subtracting 1.4 from the x component because of the rivers current. Then I get position information by integrating the velocity equations. I set the x component of the position equal to -63 (I made west positive and east negative) and then solve for t. Then I plug that t into the y component of the position and try to solve for theta. I end up with 230costheta+63sintheta=70. I tried to solve it and quickly realized it is pretty much impossible to find theta from that. So if somebody could figure out what I need to change in how I'm trying to do this problem that would be great, I have been stuck on this problem for 3 days. Last problem in my homework set. Thank you!