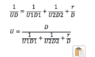A heat exchanger is to be used to heat a process liquid with....

[Tiberious]

Homework Statement

(c) A heat exchanger is to be used to heat a process liquid within the tubes using saturated steam at 100oC. The tubes have an inside diameter of 20 mm and outside diameter of 22 mm. It is estimated that the inner surface heat transfer coefficient will be 4.2 kW m-2 K-1 and the outer surface heat transfer coefficient will be 15.4 kW m-2 K-1 when the exchanger is clean. In order to allow for possible fouling during use you should assume a fouling factor of 1.12 × 10-4 m2 K W-1 will be applicable. 
Estimate:

The Attempt at a Solution

The overall heat transfer coefficient in use

R_f= 1.12∙10^(-4) m^2 K W^(-1)
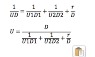
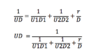
R_A= R_INNER 〖+R〗_OUTER 〖+R〗_f
R_A= 1/4.2+1/15.4+1.12=1.423 m^2 K 〖kW〗^(-1)
U= 1/R_A = 1/1.423= 0.703 kW m^2 K^(-1) Ive been provided some feedback with respect to the above answer, "But remember the U you can get from here is the U, based on average area [Uave], between inner and outer dia of the heat exchanger surface." would someone be able to explain this for me ? From the notes I have then answer should be correct.[/B]

 

[Tiberious]

Please remove the obvious error with 1.12 instead of 0.112.

 

[Chestermiller]

Your equations are pretty unreadable. Can you use LaTex please?

 

[Tiberious]

Ive never been able to figure that one out.. Ill try do some reading up, however, I've attached a screen shot of the equation for you.

 

[Chestermiller]

Ive never been able to figure that one out.. Ill try do some reading up, however, I've attached a screen shot of the equation for you.

The exact relationship should be $$\frac{1}{UD}=\frac{1}{U_iD_i}+\frac{1}{U_oD_o}+\frac{r}{D}$$where D is the diameter you use in calculating U, and for applying $U(\pi DL)$. The choice of D is at the discretion of the engineer.

 

[Tiberious]

SO, 1/UD = 1/(2.409)*(21)

2.409 Being U with the corrected 0.112 figure and D being the Average diameter between inner and outer?

 

[Chestermiller]

SO, 1/UD = 1/(2.409)*(21)

2.409 Being U with the corrected 0.112 figure and D being the Average diameter between inner and outer?

I think that would be fine.

 

[Tiberious]

Hey, went back to my lecturer with the below and it seems Ra is correct but not U. Can you check if I have followed your advise correctly.

 

[Chestermiller]

I get $$\frac{1}{U(0.021)}=\frac{1}{4.2(0.020)}+\frac{1}{15.4(0.022)}+\frac{0.112}{0.021}$$

 

[Chestermiller]

Hey, went back to my lecturer with the below and it seems Ra is correct but not U. Can you check if I have followed your advise correctly.

A reality check is: Is the overall heat transfer coefficient I calculated lower than any of the individual heat transfer coefficients that went into its calculation? If not, something is wrong.

 

[Tiberious]

Sorry I'm not following. The notes of this module have led to a great amount of confusion.

1/U(0.021) = 1/4.2*(0.020) + 1/15.4*(0.022) + 0.112/0.021

For the above, would we not transpose to remove U from the base.

Attaining: U = 1/(0.021) - 1/4.2*(0.020) + 1/15.4*(0.022) + 0.112/0.021

 

[Chestermiller]

Sorry I'm not following. The notes of this module have led to a great amount of confusion.

1/U(0.021) = 1/4.2*(0.020) + 1/15.4*(0.022) + 0.112/0.021

For the above, would we not transpose to remove U from the base.

Attaining: U = 1/(0.021) - 1/4.2*(0.020) + 1/15.4*(0.022) + 0.112/0.021

Yes, but you have to do the math correctly. And please use LaTex and/or properly apply parentheses in the denominators. In solving physics and engineering problems, the math is supposed to be a gimme.

 

[Tiberious]

Does the transposition look anything like the below.

 

[Chestermiller]

Does the transposition look anything like the below.

Not quite. The algebra still isn’t correct.

 

[Tiberious]

As we are dividing my D in the previous we should multiply when transposed. I assume this is correct.

 

[Chestermiller]

As we are dividing my D in the previous we should multiply when transposed. I assume this is correct.

Sorry. Still wrong. I'm going to transfer this thread to the Precalulus Math forum to see if they can help you better.

 

[SammyS]

Sorry. Still wrong. I'm going to transfer this thread to the Precalulus Math forum to see if they can help you better.

OK, Chet, I'll look this over.

I sure would like it if posters would use the "Image" icon in the blue banner line at the top of the reply box to display a good size image.
Post #4:

...

Post #13:

Post #15:

Starting with $\displaystyle \ \frac1{UD}=\frac1{U_1 D_1}+\frac1{U_2 D_2}+\frac r{D} \,,$ find a common denominator for the RHS and make it into a single fraction (rational expression).

Then you can "Flip" both sides.

Added in EDIT:
... but that results in a very messy expression

Simply take the reciprocal of both sides, taking more care than you did in post #13.
If you have an expression for $\ UD \,,\$ how do you solve for $\ U \,?$

Notice that the reciprocal of $\displaystyle \ \frac1 a + \frac 1 b \,,$ is not $\displaystyle \ a+b \,.$

 

[Tiberious]

Possibly something like the below ?

 

[SammyS]

Possibly something like the below ?

View attachment 229901

Definitely not. Although the issue of displaying the screen shot is MUCH improved.

A more general example.

Notice, the reciprocal of $\ \displaystyle \ \frac x a + \frac y b \,, \$ is not $\displaystyle \ \frac a x + \frac b y \,. \$

Most simply it's $\ \displaystyle \frac 1 {\displaystyle \ \frac x a + \frac y b} \,. \$

Again you were much closer with Post #13, also BTW, you didn't answer the question;

"If you have an expression for $\ UD \,,\$ how do you solve for $\ U \,?$"​

.

 

[Tiberious]

So far I've got this.

Then do we divided by D on both sides ? Removing D on the LHS. Does each term on the base of the RHS get divided by D ?

 

[SammyS]

So far I've got this.

View attachment 229903

Then do we divided by D on both sides ? Removing D on the LHS. Does each term on the base of the RHS get divided by D ?

In order: Yes. then No.

As @Chestermiller has pointed out, this now boils down to Basic Algebra/Arithmetic.

When I come up with some question as to how to perform some type computation that I haven't done in a long time, I try to check what makes sense, by using a less complicated example and/or use some numerical values.

What do you do if you are to divide a fraction like $\displaystyle \ \frac 3 8 \$ by a whole number like 2?

Hopefully, you know what to do in that case.

In your case, the denominator is a little more complicated.

Your numerator is simply $\ 1\$.
The denominator is this entire expression. $\displaystyle \ \frac1{U_1 D_1}+\frac1{U_2 D_2}+\frac r{D} \,,$

So, what do you do to divide your fraction ,$\displaystyle \ \frac{1} {\ \displaystyle{\frac1{U_1 D_1}+\frac1{U_2 D_2}+\frac r{D}}\ } \,,$ by $\ D\,?$

 

[Tiberious]

Apologies for the slow reply, I've been a little busy of late. Please see the below.

 

[SammyS]

Apologies for the slow reply, I've been a little busy of late. Please see the below.

View attachment 230450

Good!

You can now distribute the D if that helps understand how to deal with any question you now need to answer. (You do not need to distribute D if you chose not to.)

 

[Chestermiller]

Apologies for the slow reply, I've been a little busy of late. Please see the below.

View attachment 230450

Yes. Finally correct. You might consider applying the distributive rule in the denominator to multiplying D by the term in ( ).