SUMMARY
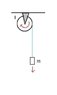
The discussion revolves around a physics problem involving a light string wrapped around a solid cylinder with a 300 g mass hanging from it. The mass falls 54 cm in 3.0 seconds, leading to the calculation of tension in the string, which is determined to be 2.9 N. The mass of the cylinder is calculated using the equations of motion and rotational dynamics, resulting in a mass of approximately 48.3 kg. Key equations used include F=ma, I=1/2(mr^2), and the relationship between linear and angular acceleration.
PREREQUISITES
- Understanding of Newton's Second Law (F=ma)
- Familiarity with rotational inertia (I=1/2(mr^2))
- Knowledge of torque and its relation to angular acceleration (τ = rF)
- Basic kinematics, particularly the equations of motion
NEXT STEPS
- Study the relationship between linear and angular motion in rotational dynamics
- Learn about torque and its applications in rotational systems
- Explore advanced kinematic equations for varying acceleration
- Investigate the principles of energy conservation in mechanical systems
USEFUL FOR
Students studying physics, particularly those focusing on mechanics and dynamics, as well as educators seeking to enhance their understanding of rotational motion and tension in strings.