A Process of Successive Approximations

[Viona]

Homework Statement

What is the Process of Successive Approximations, how I can use it?

Relevant Equations

I need to simple mathematical example to understand it, where I can find that?

I was reading in the Book: Introduction to Quantum Mechanics by David J. Griffiths. In chapter Time-Dependent Perturbation Theory, Section: Two-level system. Every thing was fine till He said He will solve this equation:

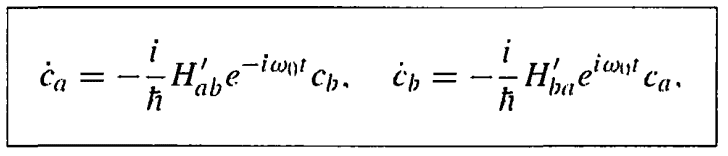
by a process of successive approximations. I have no idea what this process is and I did not find it in some books for Mathematical Methods. Please help me to understand it.

 

[Abhishek11235]

Griffiths must have explained it. Basically, you start with an initial guess of the solution and assume that solutions look like:

$$c_a=\epsilon^0c^0_a+\epsilon^1 c^1_a+\epsilon^2c^2_a+...$$
$$c_b=\epsilon^0c^0_b+\epsilon^1 c^1_b+\epsilon^3c^2_b+...$$

Here the superscript denotes the order of that element. The $\epsilon^n$ too denotes the order of elements (This is just a book-keeping device. You will set it to 1 at the end). Now, you plug these into the expression remembering that $H'$ is small, so, it is itself of the order $\epsilon$. Once you plug it, you equate terms of same order. Start by equating zeroth order terms first, then plug this solution in the equation you get after equating first order elements and so on...

 

[Viona]

It worked now, but I equated the the first order of $\epsilon$ (in the left side) with the zeroth order of $\epsilon$ (in the right side) because the right side is multiplied by $H^{'}$ which is small (of the same order of $\epsilon$). For example for the first order of $\epsilon$ i wrote:
$$ dc^{(1)}_{a} /dt =-(i /\hbar) H^{'} c^{(0)}_{b}$$
I hope this is correct.