Viona
- 49
- 12
- Homework Statement
- What is the Process of Successive Approximations, how I can use it?
- Relevant Equations
- I need to simple mathematical example to understand it, where I can find that?
I was reading in the Book: Introduction to Quantum Mechanics by David J. Griffiths. In chapter Time-Dependent Perturbation Theory, Section: Two-level system. Every thing was fine till He said He will solve this equation:
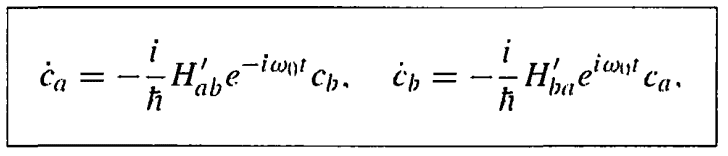
by a process of successive approximations. I have no idea what this process is and I did not find it in some books for Mathematical Methods. Please help me to understand it.
by a process of successive approximations. I have no idea what this process is and I did not find it in some books for Mathematical Methods. Please help me to understand it.