- #1
Omegared
- 14
- 0
a question on boundary layers viscosity and air seperating from a ball
I have a few questions that have to do with a viscosity on the surface of an object, the boundary layer and the boundary layer separating from the surface of a baseball!
1) my first question is if we had a stationary object let's say a baseball on a table would the baseball have a boundary layer? Or would the baseball have to be thrown for it to have a boundary layer?
2) My second question has to do with the boundary layer separating from the surface of a base ball as seen in the diagrams below (the ball is not spinning in both diagrams)

Here is a more detailed diagram
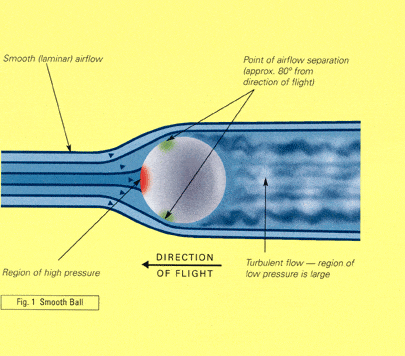
Now I read that a sphere like a baseball is a poor aerodynamic shape and if it is not spinning the boundary layer will separate similar to the figure above creating a large turbulent wake of low pressure at the back while the front has high pressure so the front to back pressure difference creates a backward force on the ball ie drag.
a) i was just curious could this pressure difference on the front and back of the ball be another application of the Bernoulli principle?
b) there was something in the explanation of the diagram above (figure2) that I just didn’t understand first of all here is how the diagram was explained:
“As smooth air flows past a ball, it experiences a uniform increase in static pressure in front of the ball, a decrease in pressure along the sides, and an increase in pressure towards the back. As the air pressure increases toward the back, the air molecules lose their ability to follow the curvature of the ball (as they try to fight the increasing pressure).
The cause of this separation happens because As the flow moves downstream from the 90° or 270° position, it encounters an increasing pressure. Whenever a flow encounters increasing pressure, we say that it experiences an adverse pressure gradient. The change in pressure is called adverse because it causes the airflow to slow down and lose momentum. As the pressure continues to increase, the flow continues to slow down until it reaches a speed of zero. It is at this point that the air no longer has any forward momentum, so it separates from the surface. separated flow creates a region of low pressure in the wake!
i) fist of all why is there a “decrease in pressure along the sides” of the ball?
ii) the above explanation also says As the flow moves downstream from the 90° or 270° position, it encounters an increasing pressure…………As the pressure continues to increase, the flow continues to slow down until it reaches a speed of zero. It is at this point that the air no longer has any forward momentum, so it separates from the surface”
Where is this Increase in Pressure along the 90° or 270° Coming From? Is it because the air is trying to fallow the curved surface but cannot because the shape of the ball is unaero dynamic?
3) this is something that really got me a bit frustrated the above explanation in green says that reason the airflow separates is because the “flow continues to slow down until it reaches a speed of zero. It is at this point that the air no longer has any forward momentum so it separates”
And yet I found another huge article (over 25 pages long) that explained the separation of air flow from the ball in a in a completely different way it says “if the air is moving fast enough past the ball the air molecules cannot move back behind the ball in a laminar or stream line flow to fill in the space behind the ball the result is turbulence. This inability of the air molecules to quickly follow behind the ball causes a partial vacuum behind the ball (I take it that by partial vacuum he is referring to the turbulence) ”
Now believe me I am far far far from an expert in physics but these two explanations regarding why the air separates from the surface of the ball seem to be totally different! The explanation in green seems to say that the air separates because it is moving too slow! And on the other hand the explanation in blue seems to be saying that the air separates because the air is moving too fast? Am I misunderstanding something?
I have a few more questions ( including the viscosity part) but so I don’t deter anyone from answering my questions I’ll post them on a different thread a little later! If anyone can help me out could you please put the number of the question your answering near your answer 1, 2a bi, bii, 3. so I don’t get confused thanks
If anyone can help me out please do I really need it and try to keep in mind I am far from an expert in physics
I have a few questions that have to do with a viscosity on the surface of an object, the boundary layer and the boundary layer separating from the surface of a baseball!
1) my first question is if we had a stationary object let's say a baseball on a table would the baseball have a boundary layer? Or would the baseball have to be thrown for it to have a boundary layer?
2) My second question has to do with the boundary layer separating from the surface of a base ball as seen in the diagrams below (the ball is not spinning in both diagrams)
Here is a more detailed diagram
Now I read that a sphere like a baseball is a poor aerodynamic shape and if it is not spinning the boundary layer will separate similar to the figure above creating a large turbulent wake of low pressure at the back while the front has high pressure so the front to back pressure difference creates a backward force on the ball ie drag.
a) i was just curious could this pressure difference on the front and back of the ball be another application of the Bernoulli principle?
b) there was something in the explanation of the diagram above (figure2) that I just didn’t understand first of all here is how the diagram was explained:
“As smooth air flows past a ball, it experiences a uniform increase in static pressure in front of the ball, a decrease in pressure along the sides, and an increase in pressure towards the back. As the air pressure increases toward the back, the air molecules lose their ability to follow the curvature of the ball (as they try to fight the increasing pressure).
The cause of this separation happens because As the flow moves downstream from the 90° or 270° position, it encounters an increasing pressure. Whenever a flow encounters increasing pressure, we say that it experiences an adverse pressure gradient. The change in pressure is called adverse because it causes the airflow to slow down and lose momentum. As the pressure continues to increase, the flow continues to slow down until it reaches a speed of zero. It is at this point that the air no longer has any forward momentum, so it separates from the surface. separated flow creates a region of low pressure in the wake!
i) fist of all why is there a “decrease in pressure along the sides” of the ball?
ii) the above explanation also says As the flow moves downstream from the 90° or 270° position, it encounters an increasing pressure…………As the pressure continues to increase, the flow continues to slow down until it reaches a speed of zero. It is at this point that the air no longer has any forward momentum, so it separates from the surface”
Where is this Increase in Pressure along the 90° or 270° Coming From? Is it because the air is trying to fallow the curved surface but cannot because the shape of the ball is unaero dynamic?
3) this is something that really got me a bit frustrated the above explanation in green says that reason the airflow separates is because the “flow continues to slow down until it reaches a speed of zero. It is at this point that the air no longer has any forward momentum so it separates”
And yet I found another huge article (over 25 pages long) that explained the separation of air flow from the ball in a in a completely different way it says “if the air is moving fast enough past the ball the air molecules cannot move back behind the ball in a laminar or stream line flow to fill in the space behind the ball the result is turbulence. This inability of the air molecules to quickly follow behind the ball causes a partial vacuum behind the ball (I take it that by partial vacuum he is referring to the turbulence) ”
Now believe me I am far far far from an expert in physics but these two explanations regarding why the air separates from the surface of the ball seem to be totally different! The explanation in green seems to say that the air separates because it is moving too slow! And on the other hand the explanation in blue seems to be saying that the air separates because the air is moving too fast? Am I misunderstanding something?
I have a few more questions ( including the viscosity part) but so I don’t deter anyone from answering my questions I’ll post them on a different thread a little later! If anyone can help me out could you please put the number of the question your answering near your answer 1, 2a bi, bii, 3. so I don’t get confused thanks
If anyone can help me out please do I really need it and try to keep in mind I am far from an expert in physics
Last edited: