A stationary photon for an observer in circular motion?

[Ookke]

Let's imagine a rocket orbiting the earth. The rocket could be any real rocket with moderate speed, so that relativistic effects are not significant, and also rocket does not experice notable centrifugal or other acceleration (so the rockets reference frame would appear almost inertial).

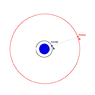
A photon orbits Earth with long enough radius so that its angular velocity matches the rockets angular velocity (see image if necessary). At any time, from rockets reference frame the photon is at constant distance directly on the side. Should we conclude that the photon is stationary when looked from rocket's frame? If yes, how the photon can exist in rocket's frame at all, having no speed (no kinetic energy) or rest mass? If no, i.e. the photon is not stationary but moves, how it actually moves relative to rocket?

I know the rocket is not strictly an inertial observer, but it's "almost" so. And in any case, the rocket is an observer (inertial or not) and the existence of a photon doesn't sound like a frame-dependent thing. I'm sure that there is a solution to this, but nothing that I can see right now. Thanks.

 

[Dale]

I know the rocket is not strictly an inertial observer, but it's "almost" so.

It is not almost inertial. As you have described it the rocket is rotating. It can measure it's rotation locally using gyroscopes or ring interferometers. The second postulate does not apply to the rockets frame and the rocket knows it.

 

[PAllen]

It's also worth noting that there is no photon orbit for the earth. The photon orbit for a mass of the Earth would require that the mass be concentrated in a diameter less than 3 cm, and the photon would orbit at a radius of about 1.5 cm.

You can imagine the photon being guided by some type of wave guide (e.g. a mirrored tube at a large enough radius to get what you want). But then, as Dalespam has already noted, the scenario is not different than asking 'where does the huge kinetic energy of distant mountains come from when I turn my head rapidly?'. In a rotating frame, inertial motion can look highly accelerated and light can travel at any speed you want.

 

[Ookke]

It can measure it's rotation locally using gyroscopes or ring interferometers.

Good point. However, during short periods of time the rocket's frame may appear pretty much like inertial one, but arguing on that would be a sidetrack. Even if the second postulate must be discarded in rocket's frame, the rocket still is an observer in the universe and the photon must be "out there" somewhere in rocket's frame in each instance of its time. I don't think that being non-inertial makes the observer's point of view completely invalid, just that the postulates don't hold.

Either the photon moves relative to rocket or it's stationary, and if it's stationary it doesn't have kinetic (or any other form of) energy. I still don't see anything wrong with this reasoning.

You can imagine the photon being guided by some type of wave guide (e.g. a mirrored tube at a large enough radius to get what you want).

Let's put it this way, orbiting Earth was a bad illustration. Both rocket and photon could be on some kind of fixed circular track, so that the angular velocities are the same.

 

[Nugatory]

Let's put it this way, orbiting Earth was a bad illustration. Both rocket and photon could be on some kind of fixed circular track, so that the angular velocities are the same.

And then coordinate systems in which the rocket observer is at rest or moving at a constant velocity are not inertial, so there's no reason to expect that $E^2=(m_0c^2)^2+(pc)^2$, hence no reason to worry about how $m_0$ and $p$ are both zero.

As an aside, you're abusing the concept of "photon" here. You don't really have a photon (this aside is a discussion for the QM forum, not the relativity forum) until it's interacted with something else. If you let go of the bogus idea that the photon is a particle, something just like the rocket ship except a lot smaller, and analyze the problem in terms of electromagnetic radiation propagating according to Maxwell's equations, the entire paradox just goes away.

 

[PAllen]

Good point. However, during short periods of time the rocket's frame may appear pretty much like inertial one, but arguing on that would be a sidetrack. Even if the second postulate must be discarded in rocket's frame, the rocket still is an observer in the universe and the photon must be "out there" somewhere in rocket's frame in each instance of its time. I don't think that being non-inertial makes the observer's point of view completely invalid, just that the postulates don't hold.

Either the photon moves relative to rocket or it's stationary, and if it's stationary it doesn't have kinetic (or any other form of) energy. I still don't see anything wrong with this reasoning.

First, note that 'existing for the rocket' (meaning the rocket could, for example, send out a probe that detects the photon and later get the information back), has nothing to do with the choice of frame or coordinates by the rocket. An astronaut on the rocket could use any frame they want, and we don't normally try to describe solar system motions in coordinates centered on (say) Zurich. Even though Zurich coordinates are effectively inertial for many local observations, they are wildly non-inertial on the scale of the solar system. It is also unremarkable that some coordinates have limited range of utility. For example, Rindler coordinates don't cover any part of spacetime outside of a wedge bounded by the Rindler horizon.

Similarly, any rotating frame has limited useful coverage. This says nothing about existence, only about problems with a particular coordinate choice. In particular, at the photon radius in your rotatiing coordinates, a line of constant coordinate position is no longer timelike - it has become 'light like' or null directed. Energy can only be defined in reference to a timelike basis. Thus energy cannot be defined relative to a vector of constant position at this radius, in these coordinates. This is not really remarkable. Physically, it is saying that you can't define the energy of a photon relative to another photon. It can only be defined relative to a material particle (which follows a timelike trajectory, defining a timelike direction for energy measurement).

 

[Dale]

Good point. However, during short periods of time the rocket's frame may appear pretty much like inertial one

The "local inertial frame" approximation requires not only a short period of time but also a small distance. The distance to get a stationary photon is, essentially by definition, not small. There is simply no avoiding it, the rocket's frame is non-inertial.

I don't think that being non-inertial makes the observer's point of view completely invalid, just that the postulates don't hold.

I agree.

Either the photon moves relative to rocket or it's stationary, and if it's stationary it doesn't have kinetic (or any other form of) energy. I still don't see anything wrong with this reasoning.

First, I would have to see the calculation showing that. Second, energy is frame variant, even with inertial frames, so I don't see the concern.

 

[Ookke]

And then coordinate systems in which the rocket observer is at rest or moving at a constant velocity are not inertial, so there's no reason to expect that $E^2=(m_0c^2)^2+(pc)^2$, hence no reason to worry about how $m_0$ and $p$ are both zero.

As an aside, you're abusing the concept of "photon" here. You don't really have a photon (this aside is a discussion for the QM forum, not the relativity forum) until it's interacted with something else.

The interaction could be arranged: the rocket can send a particle (it can use the outside inertial frame of the whole system for aiming, or someone outise can give rocket instructions how to shoot the particle) so that the particle collides with the photon, when looked from the outside inertial frame.

This collision is a local event happening in single point of spacetime, so I think all frames (inertial or not) must agree that it happens. Even if we allow m_0 and p to be zero in rocket's frame, there must be something that the particle can collide with. The photon must somehow exist, even without mass or energy.

 

[Nugatory]

The interaction could be arranged: the rocket can send a particle (it can use the outside inertial frame of the whole system for aiming, or someone outise can give rocket instructions how to shoot the particle) so that the particle collides with the photon, when looked from the outside inertial frame.

You're still talking as if you think a photon is a very small object traveling at the speed of light. It's not.

Or course an interaction can be arranged. But (and I'm repeating myself when I say that any discussion of photons, as opposed to classical electromagnetic radiation, belongs in the QM forum not here) that interaction happens at a single point. There's no photon orbit, there's no position of the photon before or after the interaction, the photon doesn't have an angular velocity, it doesn't have a trajectory, you can't even say that it existed except at the moment of the interaction. What you do have is electromagnetic radiation propagating according to Maxwell's equations until the interaction happens at a single point.

 

[PAllen]

The interaction could be arranged: the rocket can send a particle (it can use the outside inertial frame of the whole system for aiming, or someone outise can give rocket instructions how to shoot the particle) so that the particle collides with the photon, when looked from the outside inertial frame.

This collision is a local event happening in single point of spacetime, so I think all frames (inertial or not) must agree that it happens. Even if we allow m_0 and p to be zero in rocket's frame, there must be something that the particle can collide with. The photon must somehow exist, even without mass or energy.

The particle will be moving in these coordinates. It can't be stationary, or it wouldn't be following a timelike world line. Energy is measured by such a particle, and the amount measured depends on the relation between the particles 4-momentum and the photon's 4-momentum (which is perfectly well defined in such coordinates; it is just no longer (E,p) in these coordinates.). In the terms I explained in my last post, the particle's world line defines a timelike tangent vector. The dot product of the photon 4-momentum with this is the energy the particle will measure for the photon. Particles with different motion would measure different energy for the photon. None could measure zero because none can be stationary in these coordinates (at the photon radius).

[Note, in relation to Nugatory's points: I am, for the sake of discussion, willing to use the 'geometric optics' classical picture of a photon as following a null path, and having a 4-momentum. This is not accurate, but is an adequate idealization for some purposes.]

[addendum: For an example, if you use simple coordinates in which a light moving in the +x direction maintains constant u coordinate, you have (for example):

u= x-t (c=1, of course)
t' = t (I won't distinguish t' and t from here on)

The metric becomes ds^2 = du^2 + 2 dudt. The 4 momentum (E,p) transforms to (E,p-E). A 'photon' in these coordinates would have 4 momentum of (E,0), with a norm of zero per the metric as expected. If you apply the metric based norm to (E,p-E) you get√( P^2 - E^2), as expected (for the metric signature I chose; the other one would give √(E^2 - P^2)), showing this quantity is invariant. Your rotating coordinates would be more complex, but they would have the same basic features: a non-trivial metric, a funny looking 4-momentum for the photon; but the expected result of computing the energy of the photon measured by any particle. ]

 

[Ookke]

The particle will be moving in these coordinates. It can't be stationary, or it wouldn't be following a timelike world line. Energy is measured by such a particle, and the amount measured depends on the relation between the particles 4-momentum and the photon's 4-momentum (which is perfectly well defined in such coordinates; it is just no longer (E,p) in these coordinates.). In the terms I explained in my last post, the particle's world line defines a timelike tangent vector. The dot product of the photon 4-momentum with this is the energy the particle will measure for the photon. Particles with different motion would measure different energy for the photon. None could measure zero because none can be stationary in these coordinates (at the photon radius).

Thanks for posts #6 and #10, I'm trying to understand these ideas but it's a bit advanced for me. To simplify and get me on the right track, which one of these (if either) is closer to what you had in mind:

a) The photon is not stationary. Any coordinate system we try to use fails to keep the photon at constant position (constant direction and distance) relative to the rocket.

b) It is stationary, meaning that there is a coordinate system that does the job, but this coordinate system is so exotic, that being stationary in these coordinates does not imply that the photon energy is zero.

[I'm still visualizing the photon as a particle, although Nugatory (for good reasons I'm sure) was against it, but it's common in layman discussions about relativity and PAllen gave a kind of permission to do this in #10]

 

[PAllen]

Thanks for posts #6 and #10, I'm trying to understand these ideas but it's a bit advanced for me. To simplify and get me on the right track, which one of these (if either) is closer to what you had in mind:

a) The photon is not stationary. Any coordinate system we try to use fails to keep the photon at constant position (constant direction and distance) relative to the rocket.

b) It is stationary, meaning that there is a coordinate system that does the job, but this coordinate system is so exotic, that being stationary in these coordinates does not imply that the photon energy is zero.

[I'm still visualizing the photon as a particle, although Nugatory (for good reasons I'm sure) was against it, but it's common in layman discussions about relativity and PAllen gave a kind of permission to do this in #10]

(b) is mostly accurate. A key point is that a photon does not have energy as an intrinsic property (in the way rest mass is intrinsic to massive particle). Instead, in all cases, a photon's energy is only defined in reference to a particle it interacts with. Given two identically prepared photons moving in parallel, if two particles with with relative speed between them interact with the two photons, they will measure different energy. This is all normal, and coordinate independent (that is, this would be true, in Minkowski coordinates). So, a more precise statement is: even though a photon is stationary in these coordinates, it still has a defined energy in relation to any particle that might interact with it.