- #1
conectado
- 1
- 0
Hey I either have the worst physics textbook in the history of physics textbooks or i can't understand a topic.I'd appreciate if you help me decide which is it.
(Pic related is the image of the example)
First let's agree on the symbols let's call angular velocity: [itex]\omega = \frac{rxv}{||r||^2}[/itex] , angular momentum [itex]L=rxmv[/itex] and Lineal Momentum:[itex]P=mv[/itex]. Being that defined, the book attemps to proof that [itex]L[/itex] and \(\displaystyle \omega\) have generally different directions, here is the first problem i encountered, for what i know [itex]m||r||^2\omega = L[/itex] being [itex]m||r||^2[/itex] That means that Angular Velocity and Angular Momentum are parallel therefore have the same direction, the example proceed as following: 2 puntual mass are united by a rigid bar of despicable mass, therefore both have the same angular momentum. the momentum of body 1 is [itex]L_1 = r_1xm_1v_1[/itex] and it explicitly say that it's easy to see that it's contained in the plane given by [itex]P_1 P_2 \omega[/itex] (which i fail to see) being the direction perpendiculat to the line that unites [itex]P_1[/itex] with [itex]P_2[/itex] and that [itex]L_2[/itex] Has the same direction that [itex]L_1[/itex]. Therefore the Angular Impulse make an angle of [itex]\frac{\pi}{2}-\alpha[/itex] with the axis of rotation([itex]\omega[/itex]). Well that'd be an example i'd really appreciate if someone can clarify my doubts, i don't have a teacher to ask since i study by my own.
Here is a picture of the example:
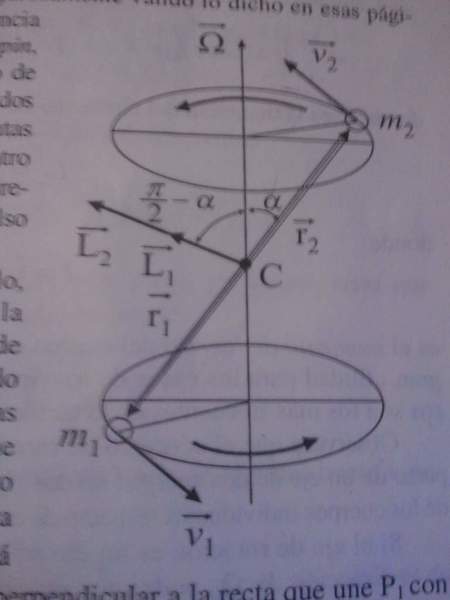
(Pic related is the image of the example)
First let's agree on the symbols let's call angular velocity: [itex]\omega = \frac{rxv}{||r||^2}[/itex] , angular momentum [itex]L=rxmv[/itex] and Lineal Momentum:[itex]P=mv[/itex]. Being that defined, the book attemps to proof that [itex]L[/itex] and \(\displaystyle \omega\) have generally different directions, here is the first problem i encountered, for what i know [itex]m||r||^2\omega = L[/itex] being [itex]m||r||^2[/itex] That means that Angular Velocity and Angular Momentum are parallel therefore have the same direction, the example proceed as following: 2 puntual mass are united by a rigid bar of despicable mass, therefore both have the same angular momentum. the momentum of body 1 is [itex]L_1 = r_1xm_1v_1[/itex] and it explicitly say that it's easy to see that it's contained in the plane given by [itex]P_1 P_2 \omega[/itex] (which i fail to see) being the direction perpendiculat to the line that unites [itex]P_1[/itex] with [itex]P_2[/itex] and that [itex]L_2[/itex] Has the same direction that [itex]L_1[/itex]. Therefore the Angular Impulse make an angle of [itex]\frac{\pi}{2}-\alpha[/itex] with the axis of rotation([itex]\omega[/itex]). Well that'd be an example i'd really appreciate if someone can clarify my doubts, i don't have a teacher to ask since i study by my own.
Here is a picture of the example:
Last edited: