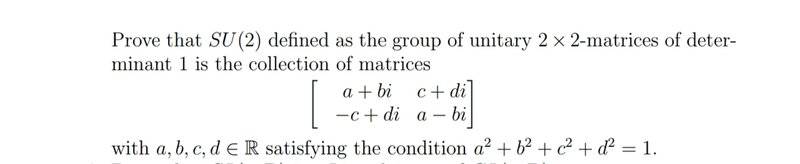Undergrad About writing a unitary matrix in another way

Click For Summary
SUMMARY

The discussion focuses on the representation of a unitary matrix, specifically how to demonstrate that a matrix of the form $$ A = \begin{bmatrix} a + bi & c + di \\ e + fi & g + hi \end{bmatrix} $$ satisfies the condition of being unitary, i.e., \(AA^\dagger = I\) with a determinant of 1. Participants highlight the necessity of establishing relationships among the matrix elements, such as \(e = -c\) and \(f = d\), to meet the unitary criteria. The conversation also touches on the potential use of the inverse matrix and its Hermitian properties to derive these relationships.

PREREQUISITES
  • Understanding of unitary matrices and their properties
  • Familiarity with matrix operations, including Hermitian and inverse
  • Knowledge of complex numbers and their representation in matrices
  • Basic linear algebra concepts, particularly determinants
NEXT STEPS
  • Study the properties of unitary matrices in linear algebra
  • Learn how to compute the Hermitian of a matrix
  • Explore the derivation of matrix inverses using standard formulas
  • Investigate the implications of determinant conditions on matrix properties
USEFUL FOR

Mathematicians, physics students, and anyone involved in quantum mechanics or linear algebra who seeks to deepen their understanding of unitary matrices and their representations.

aalma
Messages
46
Reaction score
1
It is easy to see that a matrix of the given form is actually an unitary matrix i,e, satisfying AA^*=I with determinant 1. But, how to see that an unitary matrix can be represented in the given way?
20230322_224305.jpg
 
Last edited by a moderator:
Physics news on Phys.org
Take the most general matrix,
$$
A =
\begin{bmatrix}
a + bi & c + di \\
e+ fi & g+hi
\end{bmatrix}
$$
and show that imposing ##AA^\dagger = I## requires ##e = -c##, ##f=d##, and so on.
 
Reply
  • Like
Likes aalma and topsquark
Yes, thanks. Tried to do this however got somehow long equations with these eight real numbers. guessing how it should be solved!
I also wrote the condition that the det of this matrix=1.
 
Can't you just find the inverse of the matrix using the standard formula, and then you do the hermitian of the matrix and thus figure out what the relationsships of a, b, c, ... must be?

##A^\dagger = A^{-1}##
 
Last edited:
Reply
  • Like
Likes aalma and DrClaude

Similar threads

Undergrad Why Use Gram-Schmidt to Make a Unitary Matrix?
  • · Replies 14 ·
Replies
14
Views
4K
Graduate Similarity transformation changing the determinant to 1
  • · Replies 20 ·
Replies
20
Views
3K
Undergrad Proving only 1 normalized unitary vector for normal matrix
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad Can one find a matrix that's 'unique' to a collection of eigenvectors?
  • · Replies 33 ·
2
Replies
33
Views
2K
Undergrad Matrix rank in terms of determinant polynomial
  • · Replies 14 ·
Replies
14
Views
3K
Undergrad Symbol for matrix representative of a tensor
  • · Replies 5 ·
Replies
5
Views
3K
Undergrad Can I visualize O(3) \ SO(3) in some way?
  • · Replies 4 ·
Replies
4
Views
3K
Undergrad Spectral theorem for Hermitian matrices-- special cases
  • · Replies 2 ·
Replies
2
Views
3K
Undergrad Building a Unitary Matrix from a Non-Unitary Matrix
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Does a unitary matrix have such property?
  • · Replies 4 ·
Replies
4
Views
2K