peroAlex
- 35
- 4
Hello, I'm a student of electrical engineering. This task appeared in one of the past exams. I've been using the procedure I believe should yield the correct result, however, it turns out I was wrong. Could somebody please check out where the mistake lays in my calculations?
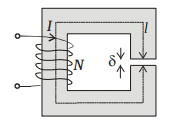
Ferromagnetic core (task assumes it is linear) has middle length of ##l = 0.2 m## and an air gap of width ##\delta = 0.001 m##. It carries a ##N = 200## winding coil conducting current ##I = 8 A##. Compute absolute value of magnetization.
I believe that ##\int H \cdot dl = 0## and ##H = \frac{B}{\mu_0} - M## should be adequate.
So, according to above mentioned equations, ##(1) H_{core}l + H_{gap}\delta = 0##. For ##H_{core}## I used ##(2) H_{core} = \frac{B}{\mu_0} - M##. Plug this into ##(1)## and so expressed magnetization ##M## should be (according to my calculations): $$ (3) M = \frac{\frac{B (l + \delta)}{\mu_0}}{l} $$
I computed B-field as with ##NI = Hl = \frac{B l}{\mu_0}## which yields ##B = 0.0032 \pi T##. Then I plugged this result into ##(3)## and obtained ##M = 8040 \frac{A}{m}## which is incorrect according to faculty provided solutions. Correct result should be ##M = 1.14 MA/m##.
Any help would be appreciated!
Homework Statement
Ferromagnetic core (task assumes it is linear) has middle length of ##l = 0.2 m## and an air gap of width ##\delta = 0.001 m##. It carries a ##N = 200## winding coil conducting current ##I = 8 A##. Compute absolute value of magnetization.
Homework Equations
I believe that ##\int H \cdot dl = 0## and ##H = \frac{B}{\mu_0} - M## should be adequate.
The Attempt at a Solution
So, according to above mentioned equations, ##(1) H_{core}l + H_{gap}\delta = 0##. For ##H_{core}## I used ##(2) H_{core} = \frac{B}{\mu_0} - M##. Plug this into ##(1)## and so expressed magnetization ##M## should be (according to my calculations): $$ (3) M = \frac{\frac{B (l + \delta)}{\mu_0}}{l} $$
I computed B-field as with ##NI = Hl = \frac{B l}{\mu_0}## which yields ##B = 0.0032 \pi T##. Then I plugged this result into ##(3)## and obtained ##M = 8040 \frac{A}{m}## which is incorrect according to faculty provided solutions. Correct result should be ##M = 1.14 MA/m##.
Any help would be appreciated!