I am aware of what OP is saying in post #5. OP is in agreement with the apparent paradox that the author of the problem, a person separate from the OP, formulated. In the author's statement of the problem, as reported by the OP in post #1, we are provided with the following reasoning
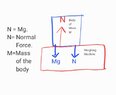
- The normal force on the person standing up on the scale is ##N=mg##.
- There are two forces acting simultaneously on the machine: the normal force and gravity
- Therefore, "the forces applied at the machine" are ##2mg.##
The task assigned by the author is to explain in detail the contradiction between statements 3 and 1. OP's initial response was
Here is my analysis.
Statement 1 is true and correct. Here ##m## is the mass of the person standing on the machine.
In statement 2 we have the assertion that there are two forces acting on the machine, gravity and the normal force. Actually there are three forces. The floor exerts a third force that is sufficient to support the weight of the machine and the person. However this third force can be ignored because it is not essential to the author's argument which in concerned with downward forces only. Nevertheless, statement 2 sets up the contradiction by the reference to gravity acting on the machine. Everybody knows that the force of gravity is ##mg##, but what ##m## is this? The author does not elaborate on purpose. However, being smart, we know that this ##m## should be the mass of the machine which is different from ##m## in statement 1.
In statement 3 the author springs the trap that was set up in statement 2. The author adds the two different masses to get ##2mg## as the downward force on the machine. This is wrong because the masses are not the same as we have seen. Having erroneously obtained ##2mg##, the author then claims that a contradiction exists with statement 1. In so doing, the author implies that this ##2mg## is the reading on the machine. It is not. The force of gravity acting on the machine does not produce a reading because it does not act at the platform where the person stands, an inference that the author wants us to make.
If I were a machine-mass denier, my argument might appear to be that the force of gravity acting on the machine does not really count, therefore the only downward force on the machine is the normal force ##N=mg## and not ##2mg.## That would appear like an attempt to say that the contradiction does not exist because ##mg+mg## is not really ##2mg## since one ##mg## can be ignored. Denial of the contradiction is not a convincing argument to someone who is grappling with these ideas. The way to do it convincingly is, as posted in #21, to show explicitly that the two masses are not additive to get ##2mg.##