blaughli
- 89
- 1
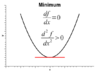
Hello. I've been watching Susskind's online Stanford lectures on classical mechanics to review the subject, and I believe he said that adding a constant to the potential energy does not change the action of a system. I see how it doesn't change the Euler-Lagrange equations and therefore doesn't affect the equations of motion (and therefore the trajectories), yet the integral of a constant is non-zero so I don't see how adding a constant to U in A = ∫(T-U)dt wouldn't change the action A. Where have I gone wrong? There seems to be an inconsistency in saying that the action changes (implying it's not at a minimum and therefore doesn't describe the true trajectory) while the E-L equations don't change (implying no change in trajectory). Thank you, sorry if I'm missing something basic and have wasted your time by not thinking about this more on my own :)