rossverg
- 11
- 0
Adding & Subtracting Vectors And Relative Velocity
Hey everyone, I am so confused with this it's not funny. This is my first time accessing a site like thisss, but I am desperate seeing as though it's school holidays atm where I am and I can't talk to my physics teacher for help. Anyhow, I hope one of you guys can help me out.
Ok I have 2 problems.
One is with adding and subtracting vectors. Ok when I have to vectors to add or subtract say
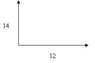
12ms-1 west + 14 ms-1 north
<IMG SRC="http://members.optushome.com.au/rossverg2002/1.JPG">
Before I do anything I draw my diagram as descbried above. The problem is that in oder to add them I need to have the vectors touching arrow-to-tail. The problem is which one of the arrows do I reverse and how do I express the new velocity (with a - sign?). Does it even matter which arrow (velocity and direction) I reverse?
Ok second problem ... I am confused with relative velocity. In my textbook there is a formula:
... I am confused with relative velocity. In my textbook there is a formula:
Velocity of a relative to b = velocity of a - velocity of b.
How do I know when to use the formula or vector diagrams? Is it only meant for velocities in a straight line? What do I do when there are 2 dimensional velcoities (like a velocity north relative to a velocity east); do I use vector diagrams instead of teh formula??
Here is an example I am stuck on with the above problem.
Car A travels at a velocity of 30.5 ms-1 north while car B travels at a velocity 25 ms-1 east. What is the velocity of B relative to A?
If I use the formula, I get 55.5 ms-1. (Velocity of b rel to a = 25 - (-30.5) which = 55ms-1)
If I use a vector diagram and find the velocity via pythagoras, I get 39.44 ms-1 N34degreesW.
Which way is the right way?? :S:S:S
Thankyou to all who help.
Your help is greatly appreciated.
Hey everyone, I am so confused with this it's not funny. This is my first time accessing a site like thisss, but I am desperate seeing as though it's school holidays atm where I am and I can't talk to my physics teacher for help. Anyhow, I hope one of you guys can help me out.
Ok I have 2 problems.
One is with adding and subtracting vectors. Ok when I have to vectors to add or subtract say
12ms-1 west + 14 ms-1 north
<IMG SRC="http://members.optushome.com.au/rossverg2002/1.JPG">
Before I do anything I draw my diagram as descbried above. The problem is that in oder to add them I need to have the vectors touching arrow-to-tail. The problem is which one of the arrows do I reverse and how do I express the new velocity (with a - sign?). Does it even matter which arrow (velocity and direction) I reverse?
Ok second problem
Velocity of a relative to b = velocity of a - velocity of b.
How do I know when to use the formula or vector diagrams? Is it only meant for velocities in a straight line? What do I do when there are 2 dimensional velcoities (like a velocity north relative to a velocity east); do I use vector diagrams instead of teh formula??
Here is an example I am stuck on with the above problem.
Car A travels at a velocity of 30.5 ms-1 north while car B travels at a velocity 25 ms-1 east. What is the velocity of B relative to A?
If I use the formula, I get 55.5 ms-1. (Velocity of b rel to a = 25 - (-30.5) which = 55ms-1)
If I use a vector diagram and find the velocity via pythagoras, I get 39.44 ms-1 N34degreesW.
Which way is the right way?? :S:S:S
Thankyou to all who help.
Your help is greatly appreciated.

Attachments
Last edited by a moderator: