georg gill
- 151
- 6
I am looking for advanced problems in statistics with answer sheet on the subjects: probability distributions where you have to rewrite the sum of variables to a new probability distribution. Advanced problems in calculating variance and expected values for probability distributions. Advanced problems for bivariate problems. Does anyone know where to find this? If you know about a learning internet site who provides this please let me know where it is. But it is also nice if you have some problems that covers this in theory books if there is an answer sheet book that is also available.
PS: I have done some research myself and I found that studypug.com provided nice theory on probabilty of permutations and combinations etc. But on the subjects that I have adressed above I am more lost on finding subjects.
An example of an assignment is:
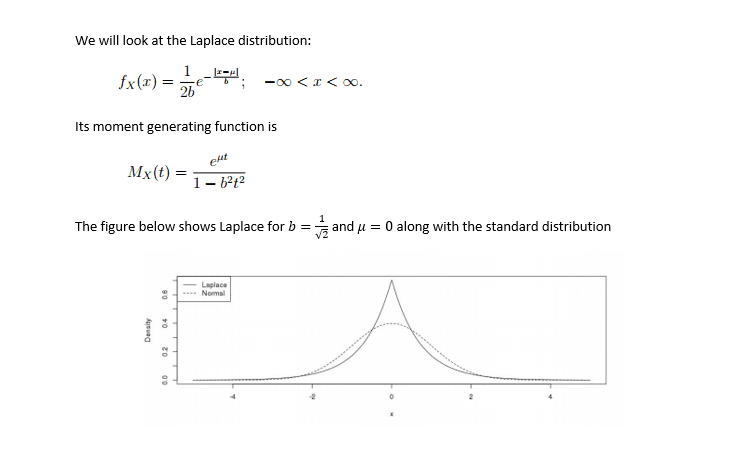

It is expecially assignments with difficulty as assignment c that I am looking for.
PS: I have done some research myself and I found that studypug.com provided nice theory on probabilty of permutations and combinations etc. But on the subjects that I have adressed above I am more lost on finding subjects.
An example of an assignment is:
It is expecially assignments with difficulty as assignment c that I am looking for.
Attachments
Last edited: