- 80
- 113
klotza submitted a new PF Insights post
All about Earth's Gravity
Continue reading the Original PF Insights Post.
All about Earth's Gravity
Continue reading the Original PF Insights Post.
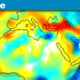
The forum discussion centers on the complexities of Earth's gravity, particularly the mathematical representation involving Legendre polynomials and spherical harmonics. Participants emphasize the importance of distinguishing between gravitational field strength and gravitational potential when discussing time dilation effects. The conversation highlights the need for clarity in explaining concepts like the geoid and gravitational anomalies, especially for varying audiences, from laypersons to physics students. Overall, the insights provided aim to enhance understanding of gravitational phenomena and their implications on time measurement.
PREREQUISITESPhysics students, educators, and anyone interested in understanding the nuances of gravitational theory and its practical implications in time measurement and geophysical studies.
... differences in the passage of time due to the differing gravitational fields ...
Both of these statements appear to be based on a common misconception. The rate of a clock does not depend on the gravitational field, but rather on the gravitational potential. Although the field is weaker at a higher potential when relating to a single central source, it is the difference in potential rather than the strength of the field which determines the time dilation. This problem seems to be limited to one paragraph, in that the following paragraphs correctly refer to the potential as determining the time dilation.... However, it is in a weaker gravitational field, so you might expect it to tick faster.
That exact point caught me off guard the day prior to this insight, I believe it was, regarding dilation of the ISS at a higher potential than the average surface of the Earth. (Zero on the gravity anomaly chart?) Being on the ISS you are moving at a faster relative velocity so clocks tick slower and being at a higher potential (and therefore less acceleration) clocks tick faster but of less magnitude than the velocity contribution. It may be the other way around? I'm not sure. This is where I need to clarify details and likely ask questions in a topic of a new thread...Jonathan Scott said:potential as determining the time dilation.
Note that higher potential doesn't always imply less gravitational acceleration. That's why it's important to understand that gravitational time dilation depends on the potential, not the gravitational acceleration.jerromyjon said:higher potential (and therefore less acceleration)
That's the direction I was heading into the shell theorem where the deeper inside the Earth you travel the effects would be opposite? Less acceleration AND lower potential?A.T. said:That's why it's important to understand that gravitational time dilation depends on the potential, not the gravitational acceleration.
klotza said:That is a good point. I will consider a better way to describe that.
M Quack said:This being a physics forum, stating the field in terms of spherical harmonics is perfectly ok, imho. Again, explicitly stating that (1-3 cos^2 theta) is the leading term in the deviation from the average might help.