Explaining Rolling Motion - Comments

[Adit Thurumalla]

How would you respond to a student who raises the issue of "frame of reference" for which the definition of "axis of rotation" is made?

For example if a student said in the context of a coin rolling on a table at a constant velocity, "What about from the frame of reference of the center of gravity of the coin? The table is moving in a straight line relative to the COG, the edge is moving without slipping at the same speed as the table, but the coin is rotating about the COG which is stationary (translationally). Why in this frame of reference should the COG not be considered the axis of rotation?"

How would/should you respond?

The COG CAN be considered as an axis of rotation. What else could one possibly consider as an axis of rotation? The mathematics would be least complicated when the axis of rotation passes through COG and perpendicular to the plane of the surface of the coin.

 

[Adit Thurumalla]

Hello all,

First post. This is really confusing to me. Let's say I had a solid wheel on the ground being driven by a specific torque without slipping. So with the center of rotation being through the middle of the wheel the Moment of Inertia would be (1/2)*mr². Yet with the center of rotation being the ground the moment of inertia changes to 3/2mr². So if angular acceleration=Torque/I why is the angular acceleration different just based on my reference frame when the wheel is driven by the same torque, it's just two ways of describing the same problem.

So I know I'm missing a lot of stuff, please help.

By considering the centre of rotation as the instantaneous point of contact, it is actually harder to visualize and do problems.Usually, where I study, we consider the axis of rotation as any line of symmetry and make necessary adjustments. This way, complications will be avoided.

 

[greypilgrim]

"I begin by defining the axis of rotation of a rigid body as the set of all points that are (instantaneously) at rest while all the other points rotate about it with angular speed ω."

Isn't that an unusual, coordinate-dependent definition of rotation? Why do you demand the axis to be at rest? If you drop this condition, the centre immediately becomes an option too.

I don't even think the argument is consistent. If I understand your definition of the IPOC correctly, each of them only exists at a point in time, so they don't even have a trajectory and the property "at rest" is meaningless.

It might be mathematically convenient to use the point of contact as the pivot point, but this conflicts with the tension within the wheel, which corresponds to the centripetal acceleration of all points about the center of mass, regardless of which inertial frame of reference is being used.

Good point. If the IPOC really is the axis of a (non-accelerated) rotation, why aren't the points on the wheel accelerated towards it?

Further abstracting OP's argument, one could describe the motion of a point along $\begin{pmatrix}t\\1\end{pmatrix}$ by an infinitesimal rotation around the axis at $\begin{pmatrix}t\\0\end{pmatrix}$ at each point in time $t$, which would be quite silly.

 

[kuruman]

"I begin by defining the axis of rotation of a rigid body as the set of all points that are (instantaneously) at rest while all the other points rotate about it with angular speed ω."

Perhaps I should have said "... the set of all points that are (instantaneously) at rest with respect to the chosen frame of reference while ... ". All motion is relative and I pick the axis of rotation to be at rest relative to whatever frame of reference one chooses to express velocities.

Isn't that an unusual, coordinate-dependent definition of rotation?

I don't think so. It is based on what I said above. It indeed is coordinate-dependent, but it is not unusual because it defines the axis of rotation in the whatever reference frame has already been chosen.

... why aren't the points on the wheel accelerated towards it?

They are. The instantaneous velocity vector of the point of interest on the rolling wheel is perpendicular to the position vector from the point of contact to the point of interest. In what direction is the centripetal acceleration relative to the point of contact?

Further abstracting OP's argument, one could describe the motion of a point along $$\begin{pmatrix}t\\1\end{pmatrix} $$by an infinitesimal rotation around the axis at $$\begin{pmatrix}t\\0\end{pmatrix}$$ at each point in time t, which would be quite silly.

I don't understand the abstraction. Can you explain it, especially the part that is silly?

 

[greypilgrim]

In what direction is the centripetal acceleration relative to the point of contact?

Sorry, I've misunderstood. I thought the IPOC was on the table, while it's actually on the wheel. But this means you're working in an upwards accelerated frame. Did you really intend to treat this in a non-inertial system?

 

[kuruman]

No, the IPOC is on the inertial frame of the table. Let P be the point of contact on the wheel and Q be the point of contact on the surface. If the wheel rolls without slipping, points P and Q are at rest relative to each another. However, point P has an upward acceleration in the inertial frame of the surface whereas point Q has zero acceleration in that same frame. The inertial frame to work in is the table surface with Q as the origin. Consider an arbitrary point S on the wheel defined by position vector $\vec{r}_S$ from point Q to S. Then the velocity of point S (relative to point Q), $\vec{V}_S$, is perpendicular to $\vec{r}_S$. If the center of the wheel is moving with velocity $\vec{V}_C$, then the angular velocity is $\omega=V_C/R$. This makes the speed $V_S=\omega~r_S=V_C(r_S/R)$.

 

[greypilgrim]

Well you can't have both

No, the IPOC is on the inertial frame of the table.

and

They are. [...] In what direction is the centripetal acceleration relative to the point of contact?

While

The instantaneous velocity vector of the point of interest on the rolling wheel is perpendicular to the position vector from the point of contact to the point of interest.

is true for both P and Q, the centripetal acceleration vectors of points on the wheel are only directed to P in its rest frame (which is not inertial, but accelerated upwards), not to Q in its rest frame (the inertial frame of the table). If a wheel rotates with constant $\omega$, the centripetal acceleration of all points is directed radially inwards, adding a constant velocity doesn't change that.

How can you claim that Q is at rest but the center of the wheel is not? They are exactly above each other at each point in time, and the center of the wheel is obviously movint to the right.

 

[kuruman]

How can you claim that Q is at rest but the center of the wheel is not?

I don't believe I made (or implied) such a claim.

In the inertial frame of the table,
1. Q is at rest because it is a point on the table.
2. P (on the rim of the wheel) is at rest with respect to the surface because the wheel is rolling without slipping.
3. The center of the wheel, C, is moving to the right (say) with speed V_C.
Therefore the center of the wheel is moving to the right with speed V_C. The translational motion of the center can also be construed as rotational motion about Q with the angular speed ω = V_C / R. The centripetal direction is not straight up as you assert, but straight down.

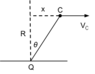
Here is a formal derivation. Consider the center C at some point in time when it is not directly above Q and is moving parallel to the surface to the right (see figure below). At that point, we have
$$x = R \tan \theta$$
$$V_C=\frac{dx}{dt}=R(\tan^2 \theta+1)\frac{d\theta}{dt}=R(\tan^2 \theta+1)\omega$$
$$\omega = \frac{V_C}{R(\tan^2 \theta+1)}$$
Point C is rotating about Q with angular speed $\omega$ as expressed above. If point C is rotating about Q, what is the centripetal direction?

When C is directly above Q, $\theta = 0$ and $\omega=V_C/ R$. What is the centripetal direction now?

 

[greypilgrim]

The centripetal direction is not straight up as you assert, but straight down.

I wasn't talking about C but P.

$$V_C=\frac{dx}{dt}$$

And since $V_C$ is constant, it follows that $a_C=\frac{d^2x}{dt^2}=0$, hence C is not accelerated, as is obvious for a linear motion with constant velocity.

If point C is rotating about Q, what is the centripetal direction?

Of course you can define straight down as the "centripetal direction", but this doesn't change the fact that C is not accelerated towards that direction as it should be in a rotation. In fact the only point on the wheel accelerated towards Q is the uppermost point of the wheel, but the magnitude of the acceleration is wrong for a rotation around Q with $\omega$. Point P is even accelerated away from Q.

 

[kuruman]

Please reread my post #43. My arguments apply to the inertial frame of reference. "Straight down" is not defined as the "centripetal direction". The centripetal direction is defined as the direction from the point of interest to the center of rotation. As seen in the figure, if point Q is the chosen center of rotation, point C rotates about Q with angular speed as derived.

... as is obvious for a linear motion with constant velocity.

Not so. It looks like you are limiting your thinking to one-dimensional motion. Examine the figure. Point C undergoes linear motion at constant velocity, true enough. Yet, relative to point Q, its velocity has a radial component (the radius being the line joining Q and C) and a tangential component. In two dimensions, point C moves radially away from Q while at the same time rotates clockwise about Q. One can always replace cartesian coordinates with polar coordinates.

 

[greypilgrim]

One can always replace cartesian coordinates with polar coordinates.

I'm not disputing that you can choose whatever coordinate system you like to describe the situation. I'm just saying that it's very unnatural to call it a "rotation", for the following reasons:

1. What's "at rest" is coordinate-dependent.
2. The points on the wheel are not accelerated towards Q.
3. The velocity of the points on the wheel have radial components, which is weird for a rotation of a rigid body.

If we choose C as the axis (dropping the restriction that an axis must be "at rest"), as most people intuitively do, none of those problems occur.

Also, you still haven't explained how you're dealing with the fact that the IPOC Q is at a different place at every point in time. How is that compatible with it being at rest?

If a point travels along $\begin{pmatrix}t\\1\end{pmatrix}$ in cartesian coordinates, you can of course express this with polar coordinates with a changing radius and a changing angle. But this is not enough to make this motion a rotation.

 

[kuruman]

If we choose C as the axis (dropping the restriction that an axis must be "at rest"), as most people intuitively do, none of those problems occur.

I agree. However, I am examining the situation from the inertial frame of the table not the non-inertial frame of the wheel.

Also, you still haven't explained how you're dealing with the fact that the IPOC Q is at a different place at every point in time. How is that compatible with it being at rest?

Please examine the drawing in post #43. Point Q is not moving relative to the surface. If Q were the IPOC, it would be drawn directly underneath point C.

But this is not enough to make this motion a rotation.

That's a matter of opinion. Consider the simpler case of a block sliding on a frictionless surface. C in the figure marks the center of mass and point Q is fixed on the surface. The block has constant angular momentum $L=mV_cR$ relative to Q. Now consider force $F$ acting on C. Clearly the angular momentum will change because the velocity will change. Changing angular momentum implies the action of a non-zero torque. Non-zero torque implies non-zero angular acceleration. Non-zero angular acceleration implies changing angular velocity. Angular velocity implies rotation about a center, in this case Q because that's the point about which the angular momentum is expressed. To me this chain of reasoning is sufficient to justify rotation even when there is no rolling motion.

 

[Robert Morphis]

You started with a seemingly arbitrary assertion about direction of rotation and application of force, then you "prove" your point by applying force to the center of the spool while pretending to apply it elsewhere using the pvc pipe.

The starting assertion should (IMO) be, applying force on one side of the axis creates rotation in one direction, applying it to the other creates rotations in the other, and applying force at the axis causes no rotation.

Yes, one certainly can analyze the problem using the IPOC, but it is not the only way to do it, and I don't really see that you have proved anything.

 

[kuruman]

Yes, one certainly can analyze the problem using the IPOC, but it is not the only way to do it, and I don't really see that you have proved anything.

It looks like you missed the point that when the force is applied at a point that is vertically even with the IPOC, there is no torque generated by that force. This level marks the threshold below which the torque is in one direction and above which it is in the opposite direction. Given that information, at what level would you say the axis of rotation is?

 

[Robert Morphis]

It looks like you missed the point that when the force is applied at a point that is vertically even with the IPOC, there is no torque generated by that force. This level marks the threshold below which the torque is in one direction and above which it is in the opposite direction. Given that information, at what level would you say the axis of rotation is?

If I apply a force at the IPOC I will either slow down or speed up the rotation, unless friction between the surface and the wheel prevents that force from actually acting on the wheel.

Use a cylinder rolling on two rails to demonstrate.

The starting assertion should (IMO) be, applying force on one side of the axis creates rotation in one direction, applying it to the other creates rotations in the other, and applying force at the axis causes no rotation.