Homework Help Overview
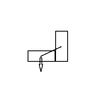
The discussion revolves around calculating the work done in displacing a brick from a horizontal position to a vertical position. The brick has specific dimensions and mass, and participants are exploring the implications of these factors on the work calculation.
Discussion Character
Approaches and Questions Raised
- Participants are questioning the initial calculations of work done, particularly the distance used in the formula. There is a focus on the center of mass (COM) and how it affects the work calculation. Some suggest that the height difference of the COM should be considered, while others express uncertainty about using COM in this context.
Discussion Status
The discussion is ongoing, with various interpretations being explored. Some participants have provided guidance on considering the COM, while others are debating the necessity of this approach. There is no explicit consensus on the method to be used for calculating work.
Contextual Notes
Participants are navigating constraints related to homework rules, which discourage providing complete solutions before the original poster has attempted the problem. There is also a mention of the brick's density and its implications, which adds complexity to the discussion.