patric44
- 308
- 40
- Homework Statement
- the relation between the filament current with the Vc .
- Relevant Equations
- I = K V^(3/2)
hi guys
i saw this experiment in an old book that uses the gas vacuum tube "thyratron" for determining the hydrogen ionization energy , the idea i guess is straight forward : we set the filament current to a specific value then the electrons starts to emit from the cathode traveling its way to the higher potential anode then we measure the corresponding anode current
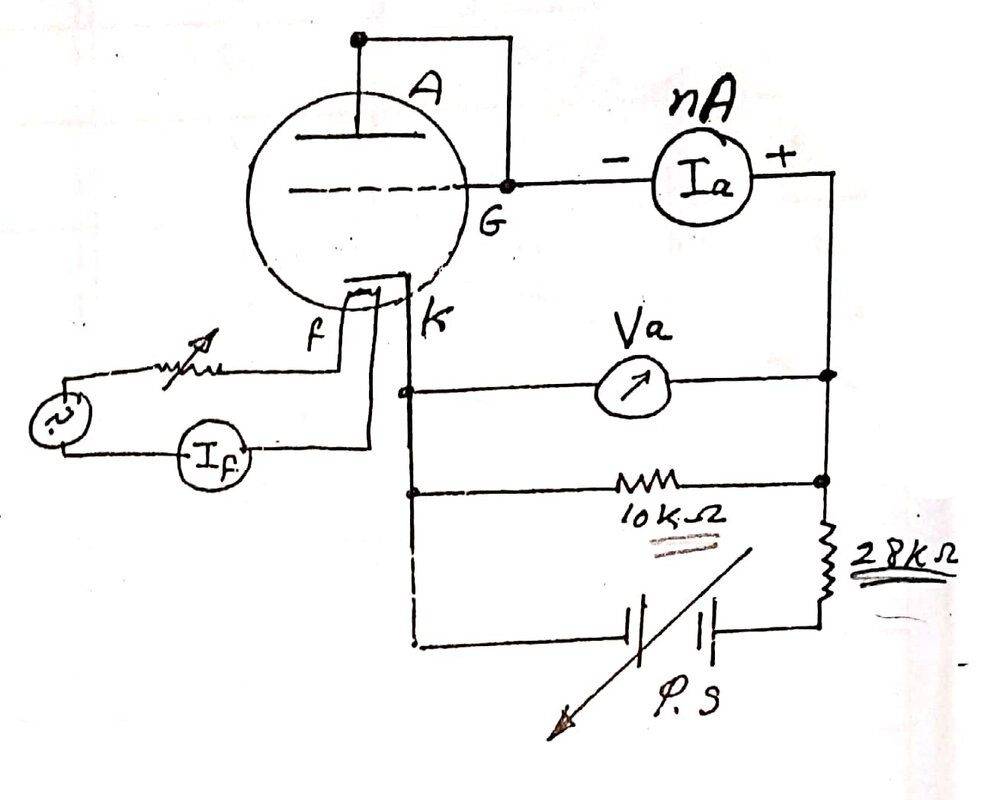
while the traveling electrons don't have enough energy to ionize the hydrogen between the plates , the anode current is subject to the relation of Child-Langmuir law :
$$I_{a} = K V^{\frac{3}{2}}_{a}$$
now the moment the electrons gain enough energy to ionize the gas this relation no longer valid and the curve deviates .
now i have a couple of questions :
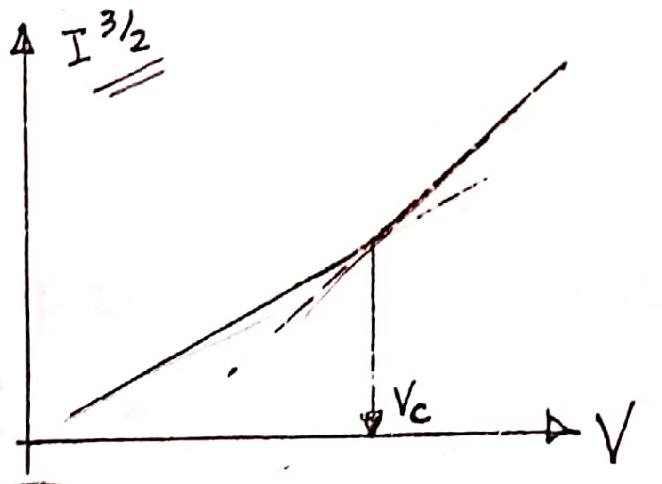
why the book states the relation that we should plot as ##I^{3/2}## with ##V## shouldn't it be ##I^{2/3}## ?!
a scanned plot from the book :
(2) the book states specifically to draw this plot at different values for the filament current to get multiple ##V_{c}## points at which the curve deviates as a function of the filament current , now this ##V_{c}## is not the ionization energy becouse the electrons has some energy from the thermionic emission in the first place , so we will draw this curve and extrapolate the curve at the value in which ##I_{f}=0## (as if the electrons gained most of its energy from the plate potential needed for ionization )
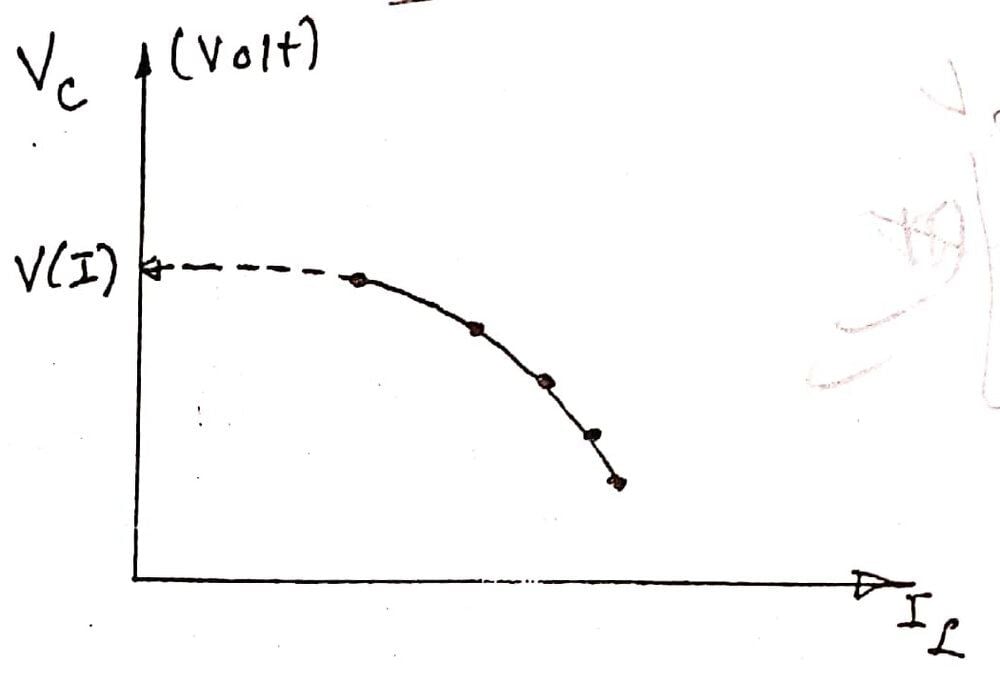
the question is could i obtain analytically the relation between the filament current and this potential ? and what is the approach for that .
thanks
i saw this experiment in an old book that uses the gas vacuum tube "thyratron" for determining the hydrogen ionization energy , the idea i guess is straight forward : we set the filament current to a specific value then the electrons starts to emit from the cathode traveling its way to the higher potential anode then we measure the corresponding anode current
while the traveling electrons don't have enough energy to ionize the hydrogen between the plates , the anode current is subject to the relation of Child-Langmuir law :
$$I_{a} = K V^{\frac{3}{2}}_{a}$$
now the moment the electrons gain enough energy to ionize the gas this relation no longer valid and the curve deviates .
now i have a couple of questions :
why the book states the relation that we should plot as ##I^{3/2}## with ##V## shouldn't it be ##I^{2/3}## ?!
a scanned plot from the book :
(2) the book states specifically to draw this plot at different values for the filament current to get multiple ##V_{c}## points at which the curve deviates as a function of the filament current , now this ##V_{c}## is not the ionization energy becouse the electrons has some energy from the thermionic emission in the first place , so we will draw this curve and extrapolate the curve at the value in which ##I_{f}=0## (as if the electrons gained most of its energy from the plate potential needed for ionization )
the question is could i obtain analytically the relation between the filament current and this potential ? and what is the approach for that .
thanks