- #1
re444
- 15
- 0
Hi every one,
Here is my question: In soil physics, knowing the relation between suction head, h, and the soil water content, S, one can derive the hydraulic conductivity, K, of that soil using a formula like:
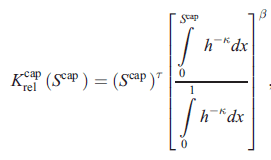
(ignore the superscripts "cap")
where in my problem, τ=0.5, κ=1, β=2.
Now what if we need the reverse procedure? If I have the relation between h and K, and want to calculate S, how it is possible?
Thanks in advance,
Mohammad
Here is my question: In soil physics, knowing the relation between suction head, h, and the soil water content, S, one can derive the hydraulic conductivity, K, of that soil using a formula like:
(ignore the superscripts "cap")
where in my problem, τ=0.5, κ=1, β=2.
Now what if we need the reverse procedure? If I have the relation between h and K, and want to calculate S, how it is possible?
Thanks in advance,
Mohammad