An integral relation in soil physics

[re444]

Hi every one,

Here is my question: In soil physics, knowing the relation between suction head, h, and the soil water content, S, one can derive the hydraulic conductivity, K, of that soil using a formula like:

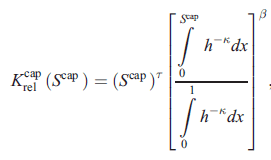
(ignore the superscripts "cap")
where in my problem, τ=0.5, κ=1, β=2.

Now what if we need the reverse procedure? If I have the relation between h and K, and want to calculate S, how it is possible?


Thanks in advance,
Mohammad

 

[SteamKing]

Iteration is one way.

You know K on the LHS of the equation, and you have h as a function of x, along with the constants tau, kappa, and beta. The integral in the denominator seems to be a fixed quantity, but the value of the integral in the numerator depends on the value of S for the upper limit.

The engineering approach, would be to assume different values of the parameter S and calculate the LHS and the RHS of the equation, or re-write the equation as LHS - RHS = 0. Then you can iterate until a particular value of S makes this relation arbitrarily close to zero.

You could probably put together a spreadsheet to calculate the value of the expression for various input values of S.

 

[re444]

Iteration is one way.

You know K on the LHS of the equation, and you have h as a function of x, along with the constants tau, kappa, and beta. The integral in the denominator seems to be a fixed quantity, but the value of the integral in the numerator depends on the value of S for the upper limit.

The engineering approach, would be to assume different values of the parameter S and calculate the LHS and the RHS of the equation, or re-write the equation as LHS - RHS = 0. Then you can iterate until a particular value of S makes this relation arbitrarily close to zero.

You could probably put together a spreadsheet to calculate the value of the expression for various input values of S.

The issue here is in the reverse procedure we don't have any knowledge about the relation between h and x (or in fact h and S), so the integrals could not be calculated. How about this?

 

[pasmith]

If I have the relation between h and K, and want to calculate S, how it is possible?

If you know h : [0,1] \to \mathbb{R}, \beta, \kappa, \tau and K, then you can calculate <br /> I(S) = \left(\frac{\int_0^S h^{-\kappa}\,dx}{\int_0^1 h^{-\kappa}\,dx}\right)^{\beta} for any 0 \leq S \leq 1 and from that you can solve <br /> K = S^\beta I(S) numerically for S. (I'm assuming here that only values of S between 0 and 1 inclusive make physical sense.)

The issue here is in the reverse procedure we don't have any knowledge about the relation between h and x (or in fact h and S), so the integrals could not be calculated. How about this?

h is a function of a real variable. If you can't determine h(x) for every x in the domain then there is no sense in which you know h. Thus you can't calculate I(S) for any S other than the trivial I(0) = 0 (if \beta &gt; 0) and I(1) = 1. If you can't calculate I(S) you have no hope of solving K = S^{\tau}I(S) for S.

 

[re444]

If you know h : [0,1] \to \mathbb{R}, \beta, \kappa, \tau and K, then you can calculate <br /> I(S) = \left(\frac{\int_0^S h^{-\kappa}\,dx}{\int_0^1 h^{-\kappa}\,dx}\right)^{\beta} for any 0 \leq S \leq 1 and from that you can solve <br /> K = S^\beta I(S) numerically for S. (I'm assuming here that only values of S between 0 and 1 inclusive make physical sense.)



h is a function of a real variable. If you can't determine h(x) for every x in the domain then there is no sense in which you know h. Thus you can't calculate I(S) for any S other than the trivial I(0) = 0 (if \beta &gt; 0) and I(1) = 1. If you can't calculate I(S) you have no hope of solving K = S^{\tau}I(S) for S.

In h(x), x is a dummy variable of integration (in calculating K , when the known relation h(S) is available, S is replaced by x in the integrands. So h(x) or h(S) is exactly what we are looking for.

 

[re444]

I've gone a bit further to get this: (assuming τ=0.5, κ=1, β=2)

\frac{\mathrm{d} }{\mathrm{d} S} \int_{0}^{S}\frac{1}{h(x))}dx=\int_{0}^{1}\frac{1}{h(x))}dx \cdot \frac{\mathrm{d} }{\mathrm{d} S} \left ( \sqrt{\frac{K_{r}}{\sqrt{S}}} \right )

\Rightarrow <br /> <br /> \frac{1}{h(S))}=\int_{0}^{1}\frac{1}{h(x))}dx \cdot \frac{\sqrt{S}\frac{dK}{dh}\cdot \frac{dh}{dS}-\frac{K}{2\sqrt{S}}}{2\sqrt{\frac{K}{\sqrt{S}}}}

now knowing the K and \frac{dK}{dh}, the last equation seems to be an ODE but in this stage I don't know what to do with the \int_{0}^{1}\frac{1}{h(x))}dx ?

Can I in someway handle that?