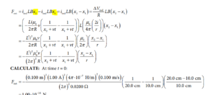mymodded
- 29
- 7
- Homework Statement
- The long, straight wire in the figure has a current i= 1.00 A flowing in it. A square loop with 10.0-cm sides and a resistance of 0.0200 ##\Omega## is positioned 10.0 cm away from the wire. The loop is then moved in the positive x-direction with a speed v = 10.0 cm/s.
Calculate the direction and the magnitude of the net force acting on the loop at the instant it starts to move.
- Relevant Equations
- ##\Delta V_{ind}=-\frac{d\Phi}{dt}##
##\Phi = \oint \vec{B} \cdot d\vec{A}##
##B_{long wire} = \frac{\mu_{0} i}{2\pi r}##
##F = ilB sin(\theta)##
this is the figure in the question.The question can be solved by first finding the induced voltage (and then the induced current), and then we can find the force on each side of the wire due to the magnetic field and subtract them from each other (since the force on the upper and lower sides are the same they cancel eachother so we only need to worry about the right and left side)
dA = 0.1 dr
##\Large \Delta V_{ind}=-\frac{d\Phi}{dt} = \frac{d}{dt}(\int_{0.1t+0.1}^{0.1t+0.2} \frac{\mu_{0} i}{2\pi r} 0.1 dr) = \frac{d}{dt}(\frac{0.1\mu_{0} i}{2\pi} (ln(0.1t+0.2) - ln(0.1t+0.1)) = \frac{0.1\mu_{0} i}{2\pi} . (\frac{0.1}{0.1+0.2} - \frac{0.1}{0.1t+0.1})##
then ##i_{ind}## is that divided by the resistance R.
then
##F_{net} = F_{right} - F_{left} = i_{ind} L B_{right} - i_{ind} L B_{left} ## where ##B= \frac{\mu_{0} i}{2\pi r}## and r is 0.1 for left and 0.2 for right and we substitute t = 0.
but the textbook solved the last part like this
which I believe is wrong, since when did F= ilbx? and when you calculate what they wrote you actually get 10^(-14)N not -16 . The answer that I got is 5*10^(-14) N so am I correct or is the textbook correct?
Attachments
Last edited: