Analytic mechanic, disk and rod

[loreberto911]

< Mentor Note -- thread moved to HH from the technical engineering forums, so no HH Template is shown >[/color]

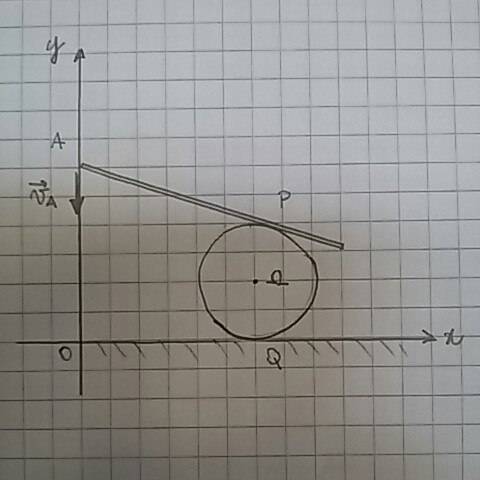
A rod rolls without creep. And the disk rolls without creep on Q. The rod can just moves on y. Which is the relation among Va and Vohm?
Va= velocity in A
My resolution:
in Q we know that velocity is zero.Q is also the instant rotation center ( disk).so the P point ( disk) is the fastest. How to bound speed in
$\Omega$ and Va?
I mean, just seeing the picture, without using the fondant formula of rigid cinematic. I could think it's like the half of Va.
Ps.it's my first article and my english isn't so good, I hope you'll understand anyway.

 

[OldEngr63]

Your picture does not define point P very well. Is it the top of the disk, or is it the tangent point? If it is the tangent point (as I suspect), it is "not the fastest point." The "fastest point" is directly on the top.

This is a kinematics problem, and as such, you need to define some more variables and write the suitable relations among them. Define a variable name for the height of point A, a variable for the distance from A to the tangent point (P?), and the angle of the bar with respect to the horizontal. Then write the equations defining the closed loop from the origin to A to P to the center of the disk to Q and back to the origin; there will be two such equations. These can be solved for what you need.

 

[loreberto911]

Your picture does not define point P very well. Is it the top of the disk, or is it the tangent point? If it is the tangent point (as I suspect), it is "not the fastest point." The "fastest point" is directly on the top.

This is a kinematics problem, and as such, you need to define some more variables and write the suitable relations among them. Define a variable name for the height of point A, a variable for the distance from A to the tangent point (P?), and the angle of the bar with respect to the horizontal. Then write the equations defining the closed loop from the origin to A to P to the center of the disk to Q and back to the origin; there will be two such equations. These can be solved for what you need.

Thanks for reply,
Point P is tangent, the question that teacher asked to me was "give me a qualitative consideration of velocity in $\Omega$"
For example the direction, and approximately the entity like "it's 1/3...2/3 of Va". The problem gives me just Va and nothing else. I tried to set problem analytically but professor said no.

 

[OldEngr63]

Afraid I can't help you if a proper mathematical formulation is not allowed.