ronniegertman
- 2
- 0
- Homework Statement
- on top of a static cylinder with a radius of R there is a cylinder with a radius of r, it is free to move, and conducts a rolling without slipping motion. When will the small cylinder detach from the larger cylinder?(R>r)
- Relevant Equations
- I want to solve this problem using effective potential energy. I think that since there is conservation of angular momentum, J always equals 0.
The tutor solved the problem using kinetic spinning energy though I find it very difficult and confusing to do so, therefore, I would like to know if there is a way to solve the problem using effective potential energy,
Veff = J2/(2mr2
below is a sketch of the problem
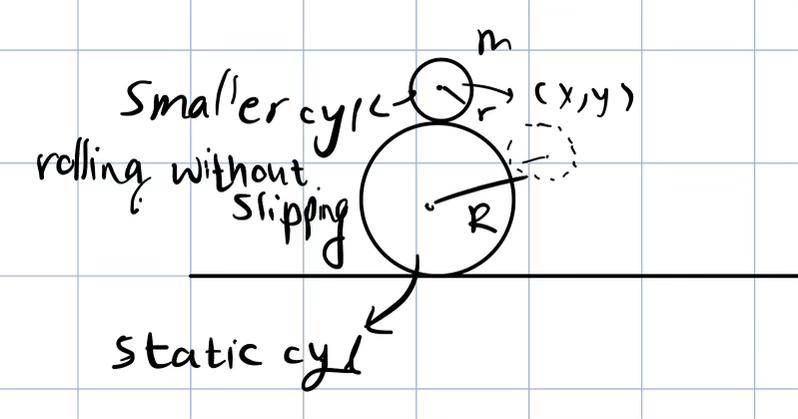
Veff = J2/(2mr2
below is a sketch of the problem