Angle observed in rest frame related to relativity

[songoku]

Homework Statement

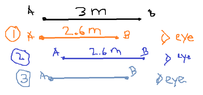
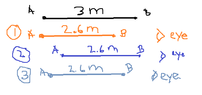
The front of a spacecraft forms a point at an angle of 60 degrees. As the spacecraft increases speed, what happens to this angle as observed in the rest frame?
A. It stays the same.
B. It decreases.
C. It increases.
D. It decreases only if the spacecraft is going to the left.
E. It decreases only if the spacecraft is going to the right

Relevant Equations

Time dilation

Length contraction

My answer is (A) since I think the motion of the spacecraft will alter the length of the spacecraft (length contraction) but not changing the orientation so the angle will stay the same

But my teacher said my answer is wrong. What is my mistake?

Thanks

 

[PeroK]

Perhaps take a fresh look at length contraction and how it relates to specific motion. Your mistake is quite fundamental and it's hard to give you a hint without giving away the answer.

 

[songoku]

Perhaps take a fresh look at length contraction and how it relates to specific motion. Your mistake is quite fundamental and it's hard to give you a hint without giving away the answer.

Is that the correct position of the angle? Thanks

 

[PeroK]

View attachment 291756
Is that the correct position of the angle? Thanks

What's the direction of motion?

 

[songoku]

What's the direction of motion?

Parallel to the spacecraft

 

[PeroK]

Parallel to the spacecraft .

So, you're assuming that the spaceship is moving at an angle of 60 degrees to some fixed axis?

 

[songoku]

So, you're assuming that the spaceship is moving at an angle of 60 degrees to some fixed axis?

Yes, that's how I interpret the question

 

[PeroK]

Yes, that's how I interpret the question

Under that assumption, the answer is clearly A. What assumption would you make if you know the answer is D?

 

[songoku]

Under that assumption, the answer is clearly A. What assumption would you make if you know the answer is D?

Is that what you mean? The angle is between a fixed point and the front tip of the spaceship and since the length of the ship contracted while moving to the left, the angle will decrease?

Thanks

 

[PeroK]

View attachment 291769
Is that what you mean? The angle is between a fixed point and the front tip of the spaceship and since the length of the ship contracted while moving to the left, the angle will decrease?

Thanks

The important thing missing from all your diagrams is an arrow indicating the direction of motion of the spaceship!

 

[songoku]

The important thing missing from all your diagrams is an arrow indicating the direction of motion of the spaceship!

I assume the spaceship is always moving in the direction it is facing. Is not correct? Like the spaceship can move horizontally to the right while its front tip making angle 60^o to the horizontal?

Thanks

 

[PeroK]

Like the spaceship can move horizontally to the right while its front tip making angle 60^o to the horizontal?

That must be the assumption if the answer is D. Bad question?

 

[songoku]

That must be the assumption if the answer is D. Bad question?

Asked the teacher and he said the answer is (C), not sure what kind of assumption needed for that one.

I would say this is crazy question. It just does not make sense to think the spaceship can move horizontally when it is not facing horizontal

 

[BvU]

Hi @songoku ,

I read the exercise statement as follows:
The front of a spaceship is a cone with a tip angle of 60 degrees (in the spaceship rest frame). The ship moves along the x-axis wrt an observer on that x-axis. What does the observer see as the cone tip angle ?

Sometimes a fancy drawing is confusing ...

$\$

 

[songoku]

Hi @songoku ,

I read the exercise statement as follows:
The front of a spaceship is a cone with a tip angle of 60 degrees (in the spaceship rest frame). The ship moves along the x-axis wrt an observer on that x-axis. What does the observer see as the cone tip angle ?

View attachment 291807
Sometimes a fancy drawing is confusing ...

$\$

Wow that's how I suppose to interpret the question. The difference is not about the drawing but about the brain capacity...

I want to ask again about length contraction (but this is not homework). Suppose I have a ruler of length 3 m and it moves with high speed to the right so the length seen by stationary observed is contracted to, let say, 2.6 m

What would be the correct diagram?

1) Position of A does not change and B is more to the left
2) Position A is more to the right and B does not change
3) A is more to the right and B is more to the left

I only know the length is contracted but I don't know which diagram will be seen by our eyes.

Thanks

 

[BvU]

Hehe, depends on WHEN ! Space and time can no longer be considered separately in this context. You have to think in terms of events that are described with a time and a place.

Suppose the observer is at rest in the origin of his coordinate system. The ruler passes by. At the time A passes the origin, the light from B that was emitted when B was at 2.6 m in the coordinate system of the observer reaches the observer. So your picture number 1.

But that's the wrong kind of reasoning. I can't even get it to work properly for me when the observer picks the moment B passes his origin...

The old and naive textbook I consulted uses three pages to treat this, nicely showing that the length contraction is symmetrical. Based on the fact that each measurement of a length involves two events that are described differently in the two frames that are linked by a Lorentz transform.

MIT gamelab have a nice relativity game. It won't help you with your time dilation conundrum, but perhaps it will with demystifying the blurring

It appears to still exist and it's fun to explore. The 'cone tip angle increase effect' sure has some interesting relatives

Other thread with some more links here

$\$

 

[songoku]

The old and naive textbook I consulted uses three pages to treat this, nicely showing that the length contraction is symmetrical.

What does it mean by symmetrical?

Thanks

 

[BvU]

Means that the guy in the moving rocket also sees a tip angle of more than 60 degrees on the spare spaceship parked on the gound next to the observer

 

[songoku]

Thank you very much for the help and explanation PeroK and BvU