hiineko
- 63
- 1
A man is standing on a 48.5 building and is looking on a second building. The angle of depression of the top and foot of the second building is 50 degrees and 80 degrees, respectively. What is the height of the second building? The height from the foot to the eye of the man is 1.5 m.
Hello guys!
I tried answering this problem and I kind of a lost of what to do here. This is my illustration, I don't know if I drew the correct illustration. Any help for answering this hard question (for me lol) will be appreciated. Thank you and God bless!
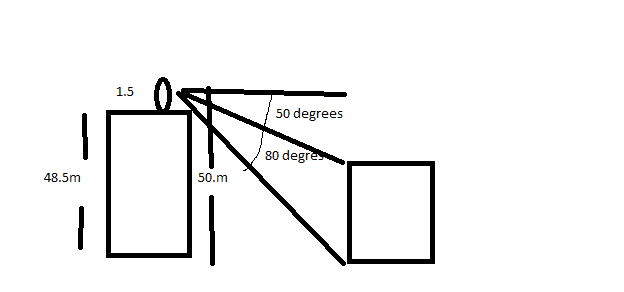
Hello guys!
I tried answering this problem and I kind of a lost of what to do here. This is my illustration, I don't know if I drew the correct illustration. Any help for answering this hard question (for me lol) will be appreciated. Thank you and God bless!