Angular magnification what is angle subtended?

[gracy]

In case of simple microscope .we take angular magnification
I know The angular magnification of an instrument is the ratio of the angle subtended at the eye when using the instrument divided by the angular size without the instrument
But what I am not getting is how this subtended angle is taken?
For example in the image below

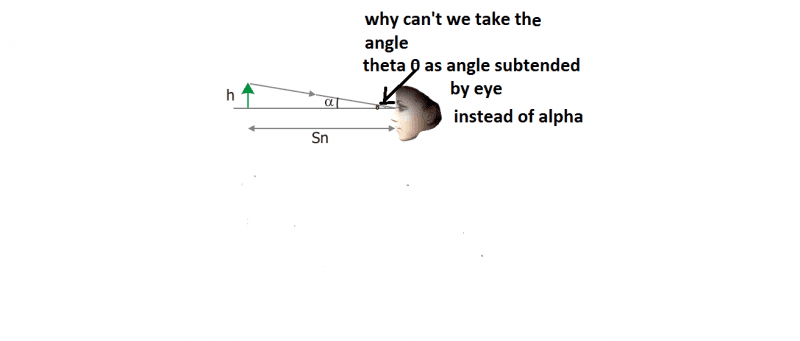
Is it because this angle theta is negligible (nearly zero)

 

[HallsofIvy]

In your picture you ask "why can't we take the angle \theta as the angle subtended rather than \alpha?". But I see NO difference between "\theta" and "\alpha". You also say "Is it because this angle theta is negligible (nearly 0)".<br /> <br /> Are you possibly thinking that the angle, measured farther out, is larger than the angle measured close to the vertex? If so, then you do not what "angle measure" <b>means</b>!

 

[gracy]

Are you possibly thinking that the angle, measured farther out, is larger than the angle measured close to the vertex?

Yes.

 

[gracy]

"angle measure" means!

Hmm... I got you point.This picture greatly explains that there is n difference between difference between "θ" and ",alpha