Compound Microscope System: Magnification Power Explained

[baseballfan_ny]

Ok so for a compound microscope system like the one below, Magnification power is $MP = M_T * M_A$. My present understanding is that $M_T$ refers to the magnification by height ratios of the object through L1, and $M_A$, in this case, refers to the ratio of unaided and aided angles of "the image of the image formed by L1" formed on the retina.

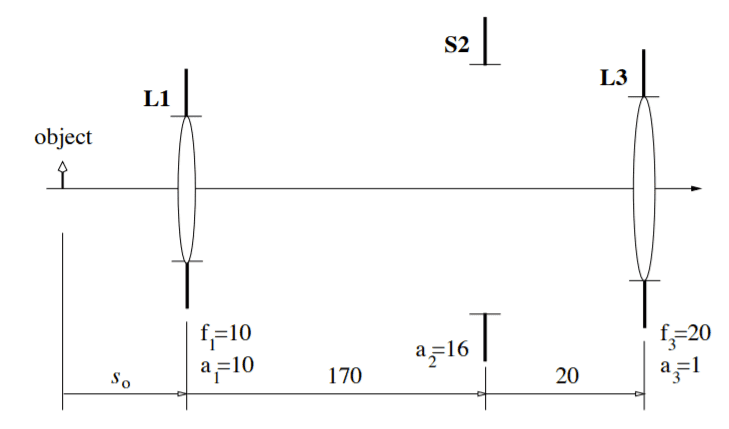
Taken from MIT OCW 2.71: https://ocw.mit.edu/courses/mechani...s-spring-2009/assignments/MIT2_71S09_ups3.pdf

Now I was kind of confused about how we could sort of cascade the $M_T$ from L1 with the $M_A$ from L3 to obtain $MP$, but I think I made sense of it by thinking about it like a system in the diagram below, and realizing that $M_T$, $M_A$ and $MP$ are all dimensionless. But I'm still not sure if my interpretation is right. I'm thinking that the Final image on the retina is an image of I2, which was just I1 angularly magnified by $M_A$. And then $M_A$ was just O laterally magnified by $M_T$. So then to obtain the total magnification of the object we would say I2 is I1 angularly magnified by $M_A$ and I1 was laterally magnified by $M_T$, so we just sort of intuitively multiply these together?

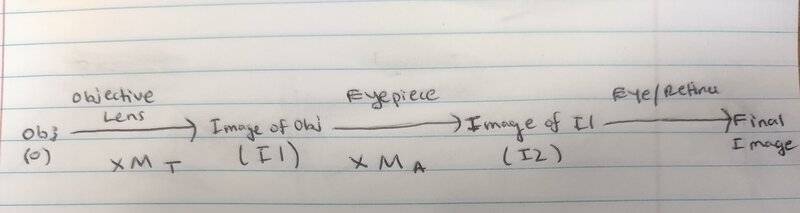
My main confusion is about this $M_A$ term and what it really is. One thing I read was that $M_A = \frac {1} {M_T}$. If that's the case, does that mean a really high angular magnification from L3 on the retina is a really small lateral magnification of the object on the retina? Ie if an object has a high angular magnification on our retina (not sure if that means breadth or something) will it appear to be really small in height on our retina? And just because it appears small on the retina, does our brain actually register it as small? Or is it just appearing small because the way our retina is curved?

 

[baseballfan_ny]

I suppose Post #1 wasn't very clear.

I guess basically what I'm confused on is what really is angular magnification and why a high angular magnification (which I assume would mean a bigger object) can be a small lateral magnification?

 

[tech99]

Yes, higher magnifying power and a reduced real image occur together.
Magnifying Power is used to describe a virtual image - one that cannot be formed on a screen. This is what you see through a telescope for instance. But you can adjust the telescope to give a real image projected on to a screen, and in this case the image is smaller than the scene being viewed.
When a virtual image is seen by the eye, remember that the eye is actually forming a real image on its retina using its own lens, and this is an inverted, reduced image.

 

[sophiecentaur]

I suppose Post #1 wasn't very clear.

I guess basically what I'm confused on is what really is angular magnification and why a high angular magnification (which I assume would mean a bigger object) can be a small lateral magnification?

As usual, when someone worries about an apparent paradox or self contradiction, it can often be put down to context.

If you use a telescope to look at the moon, the image will 'look' perhaps 50 times bigger. That's because of the angles subtended by lunar features. The eyepiece will often be adjusted to make the image appear 'at infinity, in which case you could say it will be 50 times the Moon's actual size. If you choose to focus so that the image is a metre in front of you (just as easy to see), the lateral magnification (if you actually choose to apply the definition) will be 50/350,000,000. Which of those quantities is the relevant one?

Likewise, if you project a slide on a screen with a simple lens, the lateral magnification will be, perhaps 50X but then how would you define the angular magnification? It could well be 1X.

So relax about the words used and look at what actually happens.

 

[baseballfan_ny]

When a virtual image is seen by the eye, remember that the eye is actually forming a real image on its retina using its own lens, and this is an inverted, reduced image.

Ah okay. So then (if I'm understanding this correctly) I assume the brain probably has some mechanism for reconstructing the image on the retina to be like the virtual image ... or maybe it works some other way.

If you use a telescope to look at the moon, the image will 'look' perhaps 50 times bigger. That's because of the angles subtended by lunar features. The eyepiece will often be adjusted to make the image appear 'at infinity, in which case you could say it will be 50 times the Moon's actual size. If you choose to focus so that the image is a metre in front of you (just as easy to see), the lateral magnification (if you actually choose to apply the definition) will be 50/350,000,000. Which of those quantities is the relevant one?

Oh okay. So basically (if I'm getting this) in the moon example, the lateral height of the moon image we see is probably a lot smaller than the lateral height of the moon itself. But to call that a "small image" would be overlooking the fact that the "moon" is now so much closer to our eye as a virtual image? So now what's more relevant is the angle we subtend to the image vs the angle we subtend to the object (which I suppose is angular magnification), ie how much of our field of view that the image captures vs the how much of our field of view the object captures.

So now for the definition of magnifying power of a compound microscope, I suppose the reason we use $MP = M_{T}^{objective} * M_A^{eyepiece}$ instead of $M_{T}^{objective} * M_T^{eyepiece}$ or $M_{A}^{objective} * M_A^{eyepiece}$ because $M_T$ is more relevant for the objective and $M_A$ is more relevant for the eyepiece?

 

[sophiecentaur]

So now for the definition of magnifying power of a compound microscope,

I have a feeling that the 'true' magnifying power of a microscope depends more on the user than people admit. When you buy a Lupe lens (jeweller's lens) the 'magnifying power' is often marked on the side and not the actual focal length. How much bigger the image looks (for a given lens), compared with the object is down to your near point (how good your accommodation is). The closer you can get, with the lens, the bigger the object appears - but it eventually hurts your eyes. I bet the early experimenters had pretty good eyesight in the first place, before bothering with those amazing little 'single lens' microscopes.
The optics of a telescope are more straightforward because it's clearly the angular magnification that counts and there's no advantage in focussing at anywhere than near infinity.
I think my point is that the figure quoted for a microscope may be a bit better or worse for the user and it would be difficult to estimate just what you are getting.
OTOH, a telescope or, better, binoculars can easily be tested against a distant brick wall. View it directly in one eye and through one ocular in the other. A bit of practice may be needed. You can count the number of bricks that fit in the magnified image and Bob's your uncle. There is no simple equivalent with a microscope as you may not even be able to see the object when it's that close.