Angular momentum of rotating hoop

[BroPro]

Homework Statement

Hi! See attached below a question from Kleppner's Intro to Mechanics. I calculated the angular momentum using $\mathbf L=M \mathbf R \times \mathbf V + \mathbf L_{cm}$, where $\mathbf L_{cm}$ is the angular momentum about the center of mass, but I got a different answer than the official solution.
I think both answers are correct: I calculated the angular momentum about the origin showed in the diagram, while (I think) the official solution implicitly calculated the angular momentum about the point of contact between the axle and the z axis. Is this correct? Yet it's strange for me that the angular momentum on the y axis cancels out: is this a mistake on my part, or really what happens? Why does it cancel out?

Relevant Equations

$\mathbf L=M \mathbf R \times \mathbf V + \mathbf L_{cm}$

Problem:

Official solution:

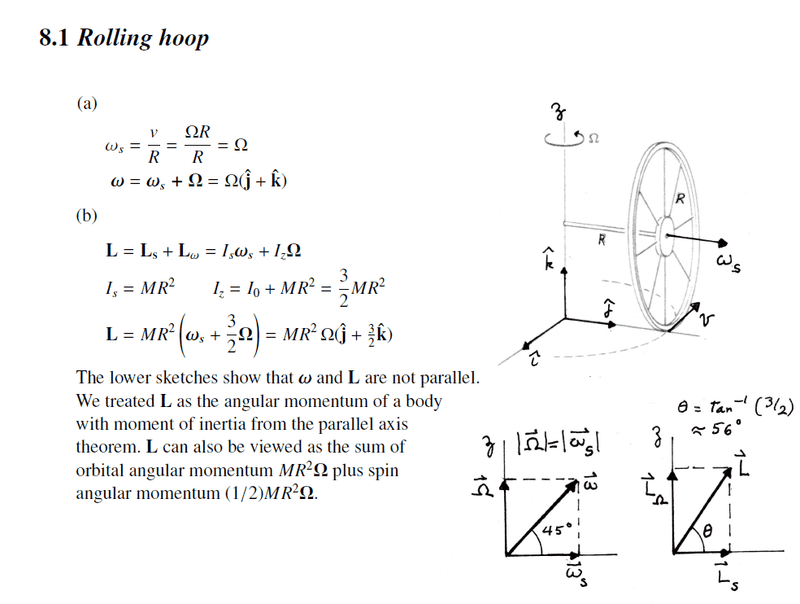
My calculation:
\begin{align*}
\mathbf L &= M \mathbf R \times \mathbf V + \mathbf L_{cm} \\
&= M R (\hat j + \hat k) \times (- \Omega R \hat i) + MR^2 \Omega \hat j \\
&= MR^2 \Omega (\hat k - \hat j + \hat j) \\
&= MR^2 \Omega \hat k
\end{align*}

 

[Orodruin]

The problem is ill posed since it fails to specify with respect to which point the angular momentum should be computed and the center of mass is not stationary.

 

[BroPro]

I've realized the answer on my own, posting it here.
I've been blindly using the $\mathbf \omega _s$ vector of the official solution, but I've realized it should point in the opposite direction to negative y. Also, in my calculation of $\mathbf L_{cm}$ I've neglected the z axis rotation of the hoop, giving the correct angular momentum of
$$\mathbf L = MR^2 \Omega (\frac{3}{2}\hat k - 2 \hat j)$$
This value is off by $-MR^2 \Omega \hat j$ from the official answer of (with correction of the sign) $\mathbf L = MR^2 \Omega (\frac{3}{2}\hat k - \hat j)$, which makes sense because my origin is off by $R$ from the origin used in the offical solution.