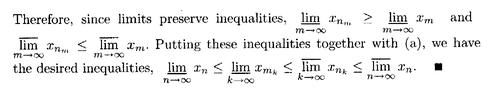Another Question on Upper and Lower Limits .... Denlinger, Theorem 2.9.6 (a)

[Math Amateur]

I am reading Charles G. Denlinger's book: "Elements of Real Analysis".

I am focused on Chapter 2: Sequences ... ...

I need help with the proof of Theorem 2.9.6 (a)Theorem 2.9.6 reads as follows:
View attachment 9250
View attachment 9251
In the above proof of part (a) we read the following:

" ... $$ \forall \ m, n \in \mathbb{N}, \ \underline{x_n} \leq \underline{ x_{n + m} } \leq \overline{ x_{n + m} } \leq \overline{ x_m }$$. Thus, $$\text{sup} \{ \underline{x_n} \ : \ n \in \mathbb{N} \} \leq \text{inf} \{ \overline{x_n} \ : \ n \in \mathbb{N} \}$$... ... "
My question is as follows:Can someone explain exactly why $$ \ \underline{x_n} \leq \underline{ x_{n + m} } \leq \overline{ x_{n + m} } \leq \overline{ x_m } \ $$ implies that $$ \ \text{sup} \{ \underline{x_n} \ : \ n \in \mathbb{N} \} \leq \text{inf} \{ \overline{x_n} \ : \ n \in \mathbb{N} \}$$ ... ... Hope that someone can help ...

Peter
===============================================================================

It may help MHB readers to have access to Denlinger's definitions and notation regarding upper and lower limits ... so I am providing access to the same ... as follows:
View attachment 9252
View attachment 9253
Hope that helps ...

Peter

 

[Opalg]

Can someone explain exactly why $$ \ \underline{x_n} \leq \underline{ x_{n + m} } \leq \overline{ x_{n + m} } \leq \overline{ x_m } \ $$ implies that $$ \ \text{sup} \{ \underline{x_n} \ : \ n \in \mathbb{N} \} \leq \text{inf} \{ \overline{x_n} \ : \ n \in \mathbb{N} \}$$ ... ...

Leaving out the two intermediate parts in that string of inequalities, you see that $\underline{x_n} \leqslant \overline{ x_m }$ (for all $m$ and $n$ in $\Bbb{N}$). Keeping $m$ fixed and letting $n$ vary, it follows that $\overline{ x_m }$ is an upper bound for the sequence $\{ \underline{x_n}\}$. Therefore $\sup\{ \underline{x_n}\} \leqslant \overline{ x_m }$.

Now let $m$ vary. That last inequality shows that $\sup\{ \underline{x_n}\}$ is a lower bound for the sequence $\{\overline{ x_m }\}$, and therefore $\sup\{ \underline{x_n}\} \leqslant \inf \{\overline{ x_m }\}$.

 

[Math Amateur]

Leaving out the two intermediate parts in that string of inequalities, you see that $\underline{x_n} \leqslant \overline{ x_m }$ (for all $m$ and $n$ in $\Bbb{N}$). Keeping $m$ fixed and letting $n$ vary, it follows that $\overline{ x_m }$ is an upper bound for the sequence $\{ \underline{x_n}\}$. Therefore $\sup\{ \underline{x_n}\} \leqslant \overline{ x_m }$.

Now let $m$ vary. That last inequality shows that $\sup\{ \underline{x_n}\}$ is a lower bound for the sequence $\{\overline{ x_m }\}$, and therefore $\sup\{ \underline{x_n}\} \leqslant \inf \{\overline{ x_m }\}$.

Thanks Opalg ...

Appreciate your help ...

Peter