(Answered) Finding new potential difference after switch is closed?

[190793]

Homework Statement

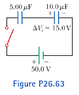
The problem is: A 10.0-μF capacitor is charged to 15.0 V. It is next connected in series with an uncharged 5.00-μF capacitor. The series combination is finally connected across a 50.0-V battery as diagrammed in Figure P26.63. Find the new potential difference across the 5.00-μF capacitor after the switch is thrown closed.

C1= 5mF and V=unknown
C2= 10mF and charged to 15V

Homework Equations

1/Ceq= 1/C1 + 1/C2
Qtot= Ceq*V
V=Q/C
Vtotal for series= V1 + V2

The Attempt at a Solution

First I found the equivalent capacitance using the first equation and found that Ceq= 3.33mF
Then I found the charge, Q, across the capacitors using the second equation and the equivalent capacitance and found that Q=1.6E-4 C.
Then I used the last equation to try to find the potential difference across C1 using 5mF as the value for the capacitance and 1.6E-4 as the charge.
My answer is wrong and I know I need to use the potential of the 10mF capacitor somewhere but I'm not sure how? Also, I'm not sure how to incorporate the switch into the problem either?

I have tried a variety of different methods and just cannot get the right answer, I'm very stuck at this point.
Thanks

 

[lightgrav]

They ask for the voltage across the 5μF capacitor, not the charge on its plate.
. . . Q/5μF should have given 33.3Volt .
The easy way: series devices divide the overall voltage between them.
Which capacitor will have more voltage (the 5 or the 10)? how many times as much?

 

[190793]

Well since the voltage is inversely proportional to the capacitance (V=Q/C) I want to say that the 5mF will have more voltage? Twice as much? I'm not sure if this is correct though.

 

[lightgrav]

yes, the small capacitor needs more voltage (x2) to hold the same Quantity of charge.
. . . so V5 = 33.3V, and V10 = 16.6V.
(The capacitors have no memory of whatever happened long before the circuit was assembled.)

 

[190793]

I see! So the fact that the 10mF capacitor was previously charged to 15V makes no difference? Thank you so much for your help the question was driving me crazy!

 

[NascentOxygen]

Note that 5μF is different from 5mF by a factor of x1000 smaller

 

[190793]

I didn't know how to get the μ symbol and mistakenly thought it could be substituted with an m! Thanks for the heads up!

 

[NascentOxygen]

yes, the small capacitor needs more voltage (x2) to hold the same Quantity of charge.
. . . so V5 = 33.3V, and V10 = 16.6V.
(The capacitors have no memory of whatever happened long before the circuit was assembled.)

This is not correct. The initial charge on the capacitors must be taken into account.

 

[190793]

This is not correct. The initial charge on the capacitors must be taken into account.

So if the 10microF capacitor had an initial charge of 15V, how can I incorporate that into finding the answer?

 

[NascentOxygen]

So if the 10microF capacitor had an initial charge of 15V, how can I incorporate that into finding the answer?

That represents an initial charge on that capacitor. When the series pair is connected across the source, equal charge is added to the plates of each capacitor until the sum of the capacitor voltages exactly opposes the source.

 

[190793]

That represents an initial charge on that capacitor. When the series pair is connected across the source, equal charge is added to the plates of each capacitor until the sum of the capacitor voltages exactly opposes the source.

Gosh I'm sorry that isn't making things very clear for me. Would the 5-microFarad capacitor take the bulk of the 50V received from the battery since the 10-microFarad capacitor already has an initial charge?
And after the battery is turned on, is the total potential difference of the circuit 50V or is it 50+15 from the initial charge?

 

[lightgrav]

oops, my bad.
It is charge, not voltage, that comes from the supply. Any charge added to the 5μF 's + plate (from the supply's +) is accompanied by the same amount of (-) charge added to its (-) plate from the 10μF 's + plate. So the 10μF capacitor always has 150μC more than the little capacitor.
The total voltage is 50V after charging.

 

[190793]

oops, my bad.
It is charge, not voltage, that comes from the supply. Any charge added to the 5μF 's + plate (from the supply's +) is accompanied by the same amount of (-) charge added to its (-) plate from the 10μF 's + plate. So the 10μF capacitor always has 150μC more than the little capacitor.
The total voltage is 50V after charging.

Ok so Ceq remains the same. Does Q?
I was under the impression that the charge is equivalent for two capacitors in series.

 

[lightgrav]

usually the capacitors are not holding charge when connected in a circuit.
Because your capacitor IS, you can't treat these as a series equivalent
of course the voltages still add, but Q₅/C₅ + Q₁₀/C₁₀ ≠ Q (1/C₅ + 1/C₁₀) , since Q₁₀≠Q₅ .

 

[190793]

Ok so if I find the charge for the 10μF capacitor, can I subtract 15C from it to find the charge of the 5μF capacitor?

 

[lightgrav]

150μC = 10μC/V ⋅ 15V

 

[190793]

I'm not sure where to go from here. Is the charge on the 5μF capacitor 1.64E-4 (the charge I found earlier using Ceq) minus the charge on the 10μF capacitor?

 

[lightgrav]

ΔV₅ + ΔV₁₀ = 35V, right?
. . . and ΔV₅ = 2 ⋅ ΔV₁₀ .

 

[190793]

Alright so V5=17.5-V10
And V10=Q/C

 

[190793]

No of course that doesn't work that just brings me back to 15!

 

[lightgrav]

to get 35 more volts, the little one needs about 22V and the big one needs about 11V more.
. . . that's only 33V more instead of the 35V you actually need. What are they, more exactly?

 

[190793]

More specifically it is 23.34 and 11.67? I found that by trial and error, what is the correct method?

 

[lightgrav]

math says ΔV₅ = 2 ΔV₁₀ , so ΔV₅ + ΔV₁₀ = 35V can be re-written as
2 ΔV₁₀ + ΔV₁₀ = 35V => 3 ΔV₁₀ = 35V => ΔV₁₀ = (35/3) V , and ΔV₅ = (70/3) V .

 

[190793]

Of course! I should have known that. Part B of the question asks for the potential difference across the big capacitor after the switch is closed which would be 50-23.3
Thank you so much for your help I FINALLY understand!