Capacitor charge in series and parallel circuit

Click For Summary

Homework Help Overview

The problem involves three capacitors with given capacitances connected to a voltage source, and the original poster seeks to determine the charge on one specific capacitor, C2. The context is within the subject area of circuits, specifically focusing on the behavior of capacitors in series and parallel configurations.

Discussion Character

  • Mixed

Approaches and Questions Raised

  • The original poster attempts to calculate the charge on capacitor C2 by considering the series connection of C1 and C2, applying the formula for equivalent capacitance. However, there is confusion regarding the configuration of the capacitors, as some participants point out that C2 and C3 are actually in parallel.

Discussion Status

Participants are actively engaging in clarifying the configuration of the capacitors. Some have suggested that the original poster reconsider the arrangement of C2 and C3, indicating that they share the same voltage and should be analyzed together. There is a back-and-forth regarding the implications of this configuration on the charge calculation.

Contextual Notes

There is an ongoing discussion about the assumptions regarding the connections of the capacitors, particularly whether C2 and C3 should be treated as parallel components affecting the charge on C2. The original poster's calculations are based on an incorrect assumption about the series connection, which has led to confusion in the charge determination.

Joshb60796
Messages
62
Reaction score
0

Homework Statement



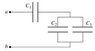
Three capacitors, with capacitances C1 = 4.0 μF, C2 = 3.0 μF, and C3 = 2.0 μF, are
connected to a 12 -V voltage source, as shown in the figure. What is the charge on
capacitor C2 ?

Homework Equations


Q=VC
Q = charge
V = voltage
C = capacitance
Ceq = equivalent capacitance

The Attempt at a Solution



C1 and C2 are in series and therefore should be summed as in Ceq=1/((1/C1)+(1/C2)) because the voltage across them will be shared proportionally. If I multiply Ceq by the voltage I get a charge of Q12 which is for both capacitors. I need to find the charge on C2 so I am multiplying the charge on both, Q12, by the proportion of C2 to C1 which is 3/4. I am getting 15.4 microCoulombs but my answer should come to 16 microCoulombs. I need help on this questions. Am I doing this correctly? Is my thought process correct?
 

Attachments

  • CapCircuit.JPG
    CapCircuit.JPG
    2.8 KB · Views: 922
Last edited:
Physics news on Phys.org
(try using the X2 button just above the Reply bos

Hi Joshb60796! :smile:

(try using the X2 button just above the Reply bos :wink:)
Joshb60796 said:
C1 and C2 are in series …

Nooo :redface: …

C2 and C3 are in parallel, and then C1 is in series with their resultant.

Try again. :smile:​
 
tiny-tim said:
Hi Joshb60796! :smile:

(try using the X2 button just above the Reply bos :wink:)


Nooo :redface: …

C2 and C3 are in parallel, and then C1 is in series with their resultant.

Try again. :smile:​


I was aware that C2 and C3 were parallel which is why I didn't include C3. Aren't C2 and C3 seeing the same voltage so if the voltage is connected for a long time C3 doesn't factor into the charge that is held on C2? I thought it was just Capacitance and Voltage that has to do with Charge, Q.
 
Joshb60796 said:
Aren't C2 and C3 seeing the same voltage …

yes :smile:
so if the voltage is connected for a long time C3 doesn't factor into the charge that is held on C2?

yes it does, C2 has to share its charge with C3 (and btw, not equally)
I thought it was just Capacitance and Voltage that has to do with Charge, Q.

yes, but you have to use the total capacitance of C2 and C3 combined to find how that combines with C1 :wink:

find the capacitance of C2 and C3,

then find the total capacitance …

show us what you get :smile:​
 

Similar threads

Two-layer dielectric, four-capacitor model vs three-capacitor model
  • · Replies 5 ·
Replies
5
Views
1K
Non-Complex Capacitor Potential Difference question
  • · Replies 9 ·
Replies
9
Views
2K
LC oscillations - two capacitors and an inductor
  • · Replies 15 ·
Replies
15
Views
1K
Capacitor Questions Charging and Discharging
  • · Replies 4 ·
Replies
4
Views
4K
Why Do Capacitors Behave Differently in Series and Parallel Configurations?
  • · Replies 20 ·
Replies
20
Views
2K
Energy stored in Capacitor Network
  • · Replies 2 ·
Replies
2
Views
14K
Charge on a capacitor in a series
  • · Replies 1 ·
Replies
1
Views
3K
Equivalent Capacitance in a circuit
  • · Replies 7 ·
Replies
7
Views
2K
(Answered) Finding new potential difference after switch is closed?
  • · Replies 23 ·
Replies
23
Views
13K
Capacitors charged in parallel
  • · Replies 3 ·
Replies
3
Views
2K