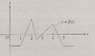Answering SAT Graphing Question: Finding Values of x from 0 to 12

[JBD2]

The Question:

The figure above shows a portion of the graph of the function f. If f(x+5) = f(x) for all values of x, then f(x) = 0 for how many different values of x between 0 and 12?

My attempt:

I have uploaded the picture of the graph so you can see what it looks like, but anyways I realize that the graph of f(x+5) is the graph of f(x) 5 units to the left, but I don't see how they can be equal to each other. I just don't understand this question in general.

 

[Mark44]

The attachment is pending approval, so we can't see the graph. The graph of y = f(x + 5) is the graph of y = f(x) translated 5 units to the left, but that's not what your problem says. It says that f(x + 5) = f(x) for all x, which means the graph is periodic with period 5 or a period that is a divisor of 5.

If f(1) = 0, then you know that f(6) = 0 and f(11) = 0, and so on.

 

[JBD2]

Ok thanks so much that makes sense now.