- #1
- 7,401
- 3,098
- TL;DR Summary
- What (changing) angular velocity will I observe?
Here's the problem setup, my student and I are stuck.
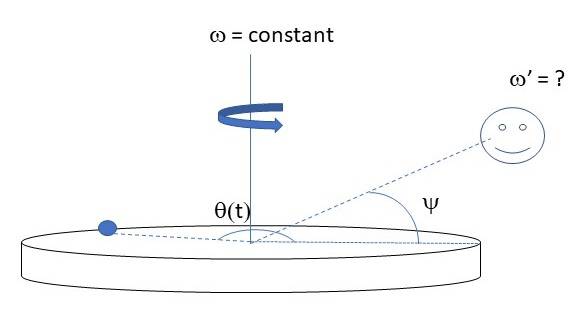
A disk is rotating at constant angular velocity ω, and we are watching a point on the rim, parameterized by the angular position θ, move. Because we are observing the motion from an inclination angle Ψ, we do not always observe the velocity ω but instead a transformed angular velocity that varies with angle θ(t) [and ψ]. This is 'simple geometry' and we figured that we could look up the formula in an astronomy context ('inclined orbits'), but for whatever reason we can't seem to figure it out. Help, please, and thanks in advance!
A disk is rotating at constant angular velocity ω, and we are watching a point on the rim, parameterized by the angular position θ, move. Because we are observing the motion from an inclination angle Ψ, we do not always observe the velocity ω but instead a transformed angular velocity that varies with angle θ(t) [and ψ]. This is 'simple geometry' and we figured that we could look up the formula in an astronomy context ('inclined orbits'), but for whatever reason we can't seem to figure it out. Help, please, and thanks in advance!