Brownie
- 1
- 0
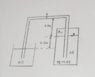
Homework Statement
The points of interest are at point A and B, I want to calculate the pressures at that point. I am working in gage pressure so we can ignore atmospheric pressure.
Homework Equations
P = pgh
P = sg x specific weight of water x height
The Attempt at a Solution
Attempting a first because I am stuck at a.
I used Pascal paradox. The level I am using is at the level of the open tank oil level. Left side is p1 and right is p2.
Pressure at point 1 is = 0 (as I’m working in gage pressure)
I’m stuck at point 2.
I think I would need a to solve b