Evaluate Problems using fluid dynamics

[RMalt]

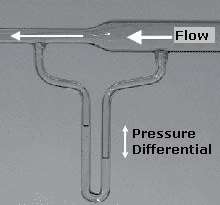
I have a diagram similar to the following. Water entering the larger end is at 20degreesC.

1. The larger end has a diameter of 8cm and Area 50.26cm2.
2. The small side has a diameter of 3cm and Area 7.0685cm2.
3. The water jet exerts a force of 87N on a flat plate at an unknown distance.
4. Assuming no frictions and a steady flow
   
5. Liquid is water

Calculate the velocity at nozzle exit.

Homework Equations

+ ∗∗+ /∗∗ = t

p1 - p2 = density/2 (v2 ^2 - v1^2)
https://wikimedia.org/api/rest_v1/media/math/render/svg/5867d9ef7ba2631627c12a000ec0096b9550c390

P = F/A

A1V1 = A2V2

The Attempt at a Solution

I have calculated the pressure at the smaller end using P=F/A . P2 = 12..3N/cm2

Using A1V1 = A2V2 I know that V2 = 7.11 * V1

I have inputted my values in the Bernoulli Equation p1 - p2 = density/2 (v2 ^2 - v1^2) , however I am ending up with both velocities as unknowns and also P1 is unknown.

I am getting stuck when I come to calculate Pressure at point 1 and Velocity at Point 2.

Any pointers or suggestions would be appreciated.

 

[Chestermiller]

Are you currently learning about macroscopic momentum balances by any chance?

 

[RMalt]

Are you currently learning about macroscopic momentum balances by any chance?

No, we have covered the Bernoulli equation, continuity of flow, the Pitot tube and the Venturi Meter.

 

[Chestermiller]

It the smaller end open to the air?

 

[RMalt]

Yes it is. I will try to update the picture of my question paper.

 

[Chestermiller]

Yes it is. I will try to update the picture of my question paper.

So, if the exit pressure is 0 Pa gauge, how do you interpret "The water jet exerts a force of 87N at the smaller end."?

 

[RMalt]

So, if the exit pressure is 0 Pa gauge, how do you interpret "The water jet exerts a force of 87N at the smaller end."?

I must have falsely interpreted my question. That was one of my mistakes that I am realising now. The 87 N is exerted on the flat plate which is a completely different story. I will update my question. I apologise for misinterpreting the question.

 

[Chestermiller]

I must have falsely interpreted my question. That was one of my mistakes that I am realising now. The 87 N is exerted on the flat plate which is a completely different story. I will update my question. I apologise for misinterpreting the question.

No big deal.

 

[akshay86]

So, if the exit pressure is 0 Pa gauge, how do you interpret "The water jet exerts a force of 87N at the smaller end."?

the force is due to the pressure of moving fluid there
F=P*A

 

[RMalt]

I still cannot use the continuity of flow theorem A1/A2 = V1/V2 or Bernoulli's equation as I do not know any velocity or Pressure at the wide end.

 

[Chestermiller]

the force is due to the pressure of moving fluid there
F=P*A

The OP already stated that the exit pressure is zero.

 

[Chestermiller]

I still cannot use the continuity of flow theorem A1/A2 = V1/V2 or Bernoulli's equation as I do not know any velocity or Pressure at the wide end.

The difficulty is interpreting what they mean by "The water jet exerts a force of 87N at the smaller end." I would interpret this as the force that the flowing fluid exerts on the body of the nozzle. But, if this is the correct interpretation, then to get what you want will require using a momentum balance on the flow in addition to the Bernoulli equation.

 

[akshay86]

I still cannot use the continuity of flow theorem A1/A2 = V1/V2 or Bernoulli's equation as I do not know any velocity or Pressure at the wide end.

pressure on the flat plate where water hits,F/A2=p2+density/2(v2^2) (when P by air=0(considering plate near to exit))

 

[Chestermiller]

pressure on the flat plate where water hits,F/A2=p2+density/2(v2^2) (when P by air=0(considering plate near to exit))

This is certainly also a reasonable interpretation, if it is in agreement with the actual problem geometry.

 

[TSny]

For part (a) I don't think the Bernoulli Eq plays a role. The force on the plate is related to the rate of loss of momentum of the stream of water as it hits the plate.

 

[RMalt]

pressure on the flat plate where water hits,F/A2=p2+density/2(v2^2) (when P by air=0(considering plate near to exit))

So I end up with : 12.3 = p2 + 1000/2(V2^2) .

Should P2 be taken as 0 in this case since it is at atmospheric pressure ?

 

[RMalt]

I came across this video while doing research however it does not match with the formula I was given earlier on.

Can anyone confirm if this video is correct ?

 

[TSny]

The video derives the correct expression for the force on the plate in terms of $\rho$, $v$ and the cross-sectional area $A$ of the stream.

(At the end of the video (at time 9:40), he forgot to divide the change in momentum by the time in order to express the force.)

 

[RMalt]

The video derives the correct expression for the force on the plate in terms of $\rho$, $v$ and the cross-sectional area $A$ of the stream.

(At the end of the video (at time 9:40), he forgot to divide the change in momentum by the time in order to express the force.)

Thanks for your insight on this matter. This means that ,F/A2=p2+density/2(v2^2) (given earlier) is incorrect ? Or am I still missing something here?

 

[Chestermiller]

The video derives the correct expression for the force on the plate in terms of $\rho$, $v$ and the cross-sectional area $A$ of the stream.

(At the end of the video (at time 9:40), he forgot to divide the change in momentum by the time in order to express the force.)

The equation I get using a momentum balance is $$F=\rho v^2 A$$

 

[TSny]

Thanks for your insight on this matter. This means that ,F/A2=p2+density/2(v2^2) (given earlier) is incorrect ? Or am I still missing something here?

I don't think this formula is relevant to relating the force on the plate to the speed of the fluid hitting the plate.

 

[TSny]

The equation I get using a momentum balance is $$F=\rho v^2 A$$

Yes. In the video, this is obtained at time 7:20.

 

[RMalt]

The equation I get using a momentum balance is $$F=\rho v^2 A$$

Using this equation the velocity will be really small ! F=ρv2A

87 = 1000 * v2 *7.0685

V2 = 0.111 cm/s . Does a value of this magnetude make sense ?

 

[TSny]

Using this equation the velocity will be really small ! F=ρv2A

87 = 1000 * v2 *7.0685

V2 = 0.111 cm/s . Does a value of this magnetude make sense ?

Watch your units.

 

[Chestermiller]

Watch your units.

I get units of force

 

[TSny]

I get units of force

Sorry, Chet. I meant to quote RmalT. I corrected it.

 

[RMalt]

v^2 = F/(density x A)

v^2 = 87/(1000 x 7.01 x10-4 )

v = 11.1 m/sMy area is in m sqaured

 

[TSny]

v^2 = F/(density x A)

v^2 = 87/(1000 x 7.01 x10-4 )

v = 11.1 m/sMy area is in m sqaured

Looks good.

 

[RMalt]

Thanks all for your help ! Now, on to the next questions !

 

[akshay86]

For part (a) I don't think the Bernoulli Eq plays a role. The force on the plate is related to the rate of loss of momentum of the stream of water as it hits the plate.

but water also exert pressure on the plate contributing to the force

 

[TSny]

but water also exert pressure on the plate contributing to the force

As I see it, the only force from the water acting on the plate is the force due to the water hitting the plate. The video in post #17 shows how to calculate this force.