Applying 2nd Kirchhoff's Law in Electrical Circuits - Homework Practice
- Thread starter Jhenrique
- Start date
-
- Tags
- Law
Click For Summary
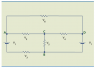
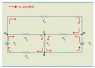
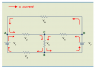
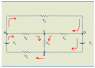
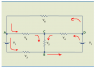
The discussion focuses on the application of the 2nd Kirchhoff's Law in electrical circuits, emphasizing the importance of consistently defining the direction of voltage drops and currents. Participants highlight that incorrect assumptions about current direction can lead to errors in equations, and they stress the need to write Kirchhoff's Voltage Law (KVL) equations correctly. The conversation also introduces the hydraulic analogy and the superposition theorem as alternative methods to understand circuit dynamics. Ultimately, the consensus is that choosing a reasonable direction for currents simplifies the analysis and leads to self-correcting solutions.
PREREQUISITES- Understanding of Kirchhoff's Voltage Law (KVL)
- Familiarity with voltage and current direction conventions
- Knowledge of the superposition theorem in circuit analysis
- Basic principles of electrical circuits and components
- Study the application of Kirchhoff's Voltage Law (KVL) in complex circuits
- Explore the hydraulic analogy in electrical circuit analysis
- Learn about the superposition theorem and its applications
- Investigate common mistakes in circuit analysis and how to avoid them
Electrical engineering students, circuit designers, and anyone looking to deepen their understanding of circuit analysis and the application of Kirchhoff's laws.
Similar threads
- · Replies 16 ·
- · Replies 1 ·
- · Replies 16 ·
- · Replies 2 ·
- · Replies 4 ·
- · Replies 2 ·
- · Replies 1 ·
- · Replies 7 ·
- · Replies 30 ·