Applying D'Alembert's principle to a bead on an elliptical hoop

[Like Tony Stark]

Homework Statement

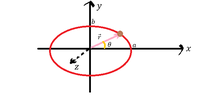
A bead of mass $m$ is placed on a vertically oriented elliptical hoop. The mass is attached to a spring of constant $k$ with its end in one of the foci. Find the equations of motion using D'Alembert's principle.

Relevant Equations

D'Alembert's principle
$F_E=-kd$, $d$: distance between mass and end of the spring

Hi
I've written D'Alembert's principle as you can see in the attached files. I computed the virtual work done by the weight and the elastic force (since the work done by the normal force is zero) and then I used the fundamental hypothesis, which states that the constraint forces can be written as the gradient of the holonomic constraints and the virtual work is zero.
The equation gets ugly, so I want to know if it's okay.

 

[haruspex]

I don't understand how you get terms like $kd\sin(\theta)$.
The spring is attached to a focus, not to the centre of the ellipse.

 

[Like Tony Stark]

I don't understand how you get terms like $kd\sin(\theta)$.
The spring is attached to a focus, not to the centre of the ellipse.

Maybe I made a mistake, but I think it's possible to write its radial and transversal components using trigonometry

 

[haruspex]

Maybe I made a mistake, but I think it's possible to write its radial and transversal components using trigonometry

Your working suggests you are defining d as the distance from the point of attachment, i.e. a focus. The magnitude of the force is therefore kd. But the diagram shows theta as the angle around the centre of the ellipse, not the angle the string subtends to the x axis.

It might clarify matters if you were to include the string in the diagram.

 

[Like Tony Stark]

Your working suggests you are defining d as the distance from the point of attachment, i.e. a focus. The magnitude of the force is therefore kd. But the diagram shows theta as the angle around the centre of the ellipse, not the angle the string subtends to the x axis.

It might clarify matters if you were to include the string in the diagram.

Ok
But apart from the elastic force, is the solution ok?

 

[haruspex]

Ok
But apart from the elastic force, is the solution ok?

I'm struggling with your notation. You seem to use ";" both for dot products and for separating elements of a vector.
Having to guess how you will correct the error I indicated above adds further uncertainty.
The $\vec{\delta r}$ vector should be tangential to the hoop, no? I don't understand how you dealt with that. It imposes a relationship between $\delta r$ and $\delta\theta$.