- #1
- 1,104
- 961
This post is also an invitation to compose problems of the presented below type.
The Lagrange–d'Alembert principle by itself is used very seldom. It is usually used to derive the Lagrange equations and that is all. But actually it is a powerful tool in nonholonomic mechanics.
As an example consider a problem which is interesting by itself.
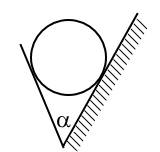
A chute is formed by two planes. The angle between the planes equals ##\alpha\in(0,\pi)## and it does not depend on time. The planes intersect by a horizontal line ##\ell##. The line ##\ell## does not change its position in the space during the time.
One of the planes is fixed while other plane moves in horizontal direction along the line ##\ell##. The velocity of this plane is a given function ##\boldsymbol u=\boldsymbol u(t)##.
Then one puts a homogeneous ball inside the chute. The ball does not slip by the both planes. Find the acceleration of the center of the ball.
The answer is
$$\frac{\dot u}{\frac{mr^2}{J}\Big(1-\cos\alpha\Big)+2},\quad J=2mr^2/5.$$
Here ##r## is a radius of the ball; ##m## is its mass.
Let us now sketch the solution by means of the Lagrange–d'Alembert principle.
Let ##S## stand for the center of the ball; ##A## stand for the contact point of the ball and the moving plane and let ##B## be the contact point of the ball and the fixed plane.
The conditions of non-slipness are
$$\boldsymbol v_S+\boldsymbol \omega\times \boldsymbol {SA}=\boldsymbol u;\quad\boldsymbol v_S+\boldsymbol \omega\times \boldsymbol {SB}=0.$$
Here ##\boldsymbol \omega## is the angular velocity of the ball.
The Lagrange–d'Alembert principle is
$$(J\boldsymbol{\dot\omega},\boldsymbol\xi)+(m\boldsymbol{\dot v}_S,\boldsymbol\gamma)=0.$$
This equation must be satisfied for all virtual displacements ##\boldsymbol\xi,\boldsymbol\gamma## such that
$$\boldsymbol \gamma+\boldsymbol \xi\times \boldsymbol {SA}=0;\quad\boldsymbol \gamma+\boldsymbol \xi\times \boldsymbol {SB}=0.$$These are the equations of motion. They allow to accomplish the solution of the problem.
The gain of using the Lagrange–d'Alembert principle is as follows. The equations of motion do not contain reaction forces at points ##A,B##. Moreover these reactions can not be defined uniquely.
Note also that if ##\boldsymbol u=0## then the problem is holonomic.
The Lagrange–d'Alembert principle by itself is used very seldom. It is usually used to derive the Lagrange equations and that is all. But actually it is a powerful tool in nonholonomic mechanics.
As an example consider a problem which is interesting by itself.
A chute is formed by two planes. The angle between the planes equals ##\alpha\in(0,\pi)## and it does not depend on time. The planes intersect by a horizontal line ##\ell##. The line ##\ell## does not change its position in the space during the time.
One of the planes is fixed while other plane moves in horizontal direction along the line ##\ell##. The velocity of this plane is a given function ##\boldsymbol u=\boldsymbol u(t)##.
Then one puts a homogeneous ball inside the chute. The ball does not slip by the both planes. Find the acceleration of the center of the ball.
The answer is
$$\frac{\dot u}{\frac{mr^2}{J}\Big(1-\cos\alpha\Big)+2},\quad J=2mr^2/5.$$
Here ##r## is a radius of the ball; ##m## is its mass.
Let us now sketch the solution by means of the Lagrange–d'Alembert principle.
Let ##S## stand for the center of the ball; ##A## stand for the contact point of the ball and the moving plane and let ##B## be the contact point of the ball and the fixed plane.
The conditions of non-slipness are
$$\boldsymbol v_S+\boldsymbol \omega\times \boldsymbol {SA}=\boldsymbol u;\quad\boldsymbol v_S+\boldsymbol \omega\times \boldsymbol {SB}=0.$$
Here ##\boldsymbol \omega## is the angular velocity of the ball.
The Lagrange–d'Alembert principle is
$$(J\boldsymbol{\dot\omega},\boldsymbol\xi)+(m\boldsymbol{\dot v}_S,\boldsymbol\gamma)=0.$$
This equation must be satisfied for all virtual displacements ##\boldsymbol\xi,\boldsymbol\gamma## such that
$$\boldsymbol \gamma+\boldsymbol \xi\times \boldsymbol {SA}=0;\quad\boldsymbol \gamma+\boldsymbol \xi\times \boldsymbol {SB}=0.$$These are the equations of motion. They allow to accomplish the solution of the problem.
The gain of using the Lagrange–d'Alembert principle is as follows. The equations of motion do not contain reaction forces at points ##A,B##. Moreover these reactions can not be defined uniquely.
Note also that if ##\boldsymbol u=0## then the problem is holonomic.
Last edited: