- #1
Better WOrld
- 80
- 1
Homework Statement
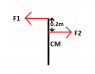
As shown in the attached figure, 2 forces ##F_1=3N## and ##F_2=5N## are applied on the rod of mass ##1## kg.The separation between the points of application of the 2 forces is 0.2 m. If the rod undergoes only translational motion, find the length of the rod.
Note that both the forces pass above the CM of the rod.Also, the rod is in the vertical plane ie gravity passes through its CM along the rod itself.
Homework Equations
The Attempt at a Solution
I first tried the problem by taking torque of ##F_1## and ##F_2## about the CM and equating it with ##0## since the angular acceleration is 0. On solving, I got the correct answer: the length of the rod is ##1m##. However, when I tried to take torque about the top of the rod (ie the point of application of ##F_1##) I get a result I can't understand.
$$0 \times F_1+ 0.2 \times F_2+\dfrac{l}{2} \times g=\dfrac{ml^2}{3} \alpha$$
$$0+1+0=0$$
$$1=0$$ since ##\alpha## of any point on the rod about the CM is ##0##.
I just cannot understand the flaw with my reasoning, and would be truly grateful for any assistance with my second method. Many thanks in advance!