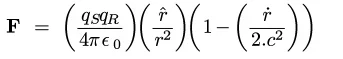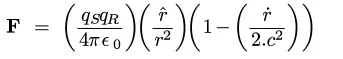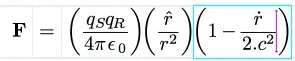Applying the Gauss (1835) formula for force between 2 parallel DC currents

[stovenn]

TL;DR

I am using Gauss's 1835 formula to try and derive the expression for the perpendicular force between two infinitely-long, parallel wires carrying steady DC currents. I obtain a formula that looks the correct shape and pattern but gives the wrong direction and magnitude for the force.

Please can anyone either:-

(1) point me to a derivation of the perpendicular force (Fy) between two very long parallel wires carrying steady currents utilising the formula of Gauss for the force F along the line r between 2 charges?

Or alternatively (2) point out where I have gone wrong in my method?

I am having problems with calculating the direction and magnitude of the force as expected from modern (Biot-Savart-Maxwell-Lorentz) formula.

Here is my method and results so far:-

This wikipedia page (https://en.wikipedia.org/wiki/Weber_electrodynamics) indicates that Gauss's formula is the same as Weber's but without the final acceleration terms:-

F=(qs.qr/4.pi.e0.r^2).( 1 - (1/2.c^2)*(dr/dt)^2 )...where dr/dt is the radial velocity.

I am using dr/dt=(Vr-Vs)*cosTheta where Vs, Vr are the velocities (in the x-direction) of the source and receiving charges. Theta is the angle between the x-axis and line r connecting the 2 charges and for a given source position P at distance X along the x-axis from the receiver theta is given by cosTheta=(-X/r).

I obtain an expression for Fy for a source charge at [X,0] and a receiver charge at [0,h]...
=(qs.qr/4.pi.e0.r^2).(h/r).( 1 - (1/2.c^2)*(dr/dt)^2 )
= (qs.qr/4.pi.e0.r^2).(h/r).( 1 - (1/2.c^2)*(Vs^2 + Vr^2 -2.Vr.Vs)*(X^2/r^2) )

Then I calculate the net Fy force over the 4 interactions between two "current elements" (source proton or source drift electron) and (receiver proton or receiver drift electron):-
Fy= (qs.qr/4.pi.e0).(hX^2/r^5).( Vr.Vs/c^2)

Integrating (hX^2/r^5) over -infinity<x<+infinity -->(2/3h)

So the total force exerted by the source wire upon the receiver current element (divided by the number of source current elements per unit length of wire):-
FY= (qs.qr/4.pi.e0).(2/3h).( Vr.Vs/c^2)
= (qs.qr/2.pi.h.e0).(1/3).( Vr.Vs/c^2).

And if the number of source current elements per unit length of wire is the same in both wires then FY also indicates the force received per unit length of the receiver wire.
= = = = = = =
Compared to the result from textbook formulae this value of FY is in the opposite direction and only (1/3) of the correct magnitude.

 

[Dale]

the formula of Gauss for the force F along the line r between 2 charges

Which formula are you referring to here?

 

[stovenn]

Which formula are you referring to here?

Hi thanks for your attention.

TLDR: I have actually solved my primary goal of demonstrating that the Gauss equation gives the same result as the textbooks by using a different equation than the one I derived and used above.

But for fullness here is what happened...
In my original post I started with the Weber formula

which is Eqtn (4) in the wikipedia article: https://en.wikipedia.org/wiki/Weber_electrodynamics.

That article presents an alternative equivalent form of the Weber equation as Eqtn (7):

.

Later the article points out that, when a=0 so Eqtn (7) becomes equivaent to Gauss's 1835 equation, Eqtn (2):

I took this to mean that I could use the Weber Eqtn (4), and simply drop the acceleration term (r.r_doubledot/c^2) therein to obtain an alternative equivalent to the Gauss formula, which I shall call "Eqtn (4.2)":

(4.2).

Using this Eqtn (4.2) I ran into the problems described in my original post.

= = = = = = = = = = = = = = = = = = = = = = =

However, I have subsequently tried using the first-presented form of the Gauss equation - Eqtn (2) and it all works out as expected - giving exactly the same result as the textbooks. To confirm this was my primary goal.

Presumably either my logic was faulty in deriving equation (4.2) and/or I made mistakes in applying it.
It would be interesting (but not so highly-important for me right now) to find where I went wrong on that path.

PS my apologies, I haven't found out yet how to use Latex/Mathjax in this forum.

 

[berkeman]

PS my apologies, I haven't found out yet how to use Latex/Mathjax in this forum.

I sent you a DM just now with some tips.

 

[stovenn]

I sent you a DM just now with some tips.

Many thanks!

I had used Mathjax some time ago.

It was the need to refresh the browser which had evaded me! (And the ability to Preview!!, and escape from Preview!!!).

 

[TSny]

Equation (6) in the link reads $$\ddot r = \frac{\mathbf{r}\cdot \mathbf{\ddot{r}}}{r} - \frac{(\mathbf{r \cdot \dot{r}})^2}{r^3} + \frac{\mathbf{r \cdot \dot{r}}}{r} = \frac{\mathbf{r}\cdot \mathbf{a}}{r} - \frac{(\mathbf{r \cdot \dot{r}})^2}{r^3} + \frac{\mathbf{r \cdot \dot{r}}}{r}$$ When the relative acceleration $\mathbf{a} = 0$, only the first term on the far right is zero. The other two terms are generally nonzero. So, when $\mathbf{a} = 0$, you cannot assume $\ddot{r} = 0$. The Weber equation (4) does not reduce to your equation (4.2) when $\mathbf{a} = 0$. Instead, equation (4) with $\mathbf{a} = 0$ reduces to the Gauss equation (2).

You should find that using the Gauss equation for the 4 interactions yields the correct net force per unit length on the "receiver" wire.

 

[stovenn]

Equation (6) in the link reads $$\ddot r = \frac{\mathbf{r}\cdot \mathbf{\ddot{r}}}{r} - \frac{(\mathbf{r \cdot \dot{r}})^2}{r^3} + \frac{\mathbf{r \cdot \dot{r}}}{r} = \frac{\mathbf{r}\cdot \mathbf{a}}{r} - \frac{(\mathbf{r \cdot \dot{r}})^2}{r^3} + \frac{\mathbf{r \cdot \dot{r}}}{r}$$ When the relative acceleration $\mathbf{a} = 0$, only the first term on the far right is zero. The other two terms are generally nonzero. So, when $\mathbf{a} = 0$, you cannot assume $\ddot{r} = 0$. The Weber equation (4) does not reduce to your equation (4.2) when $\mathbf{a} = 0$. Instead, equation (4) with $\mathbf{a} = 0$ reduces to the Gauss equation (2).

You should find that using the Gauss equation for the 4 interactions yields the correct net force per unit length on the "receiver" wire.

Aha! I see now how I slipped up by assuming that $\mathbf{a} = 0$ implies $\ddot{r} = 0$.

I had indeed subsequently gotten the correct force using the Gauss Equation (2).

Many thanks for clarifying this :)