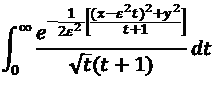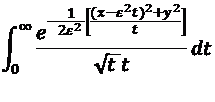Discussion Overview
The discussion revolves around the approximation of one function by another as both variables x and y approach infinity. Participants explore the conditions under which this approximation holds, the behavior of integrals involved, and the potential for measuring the error of the approximation.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant questions whether the integrals involved converge, suggesting that they do not due to the behavior of the integrands as x and y increase.
- Another participant acknowledges an error in their initial formulation of the integrals and provides corrected expressions, indicating a relationship between x and y.
- Some participants discuss the behavior of the functions f1 and f2, noting that f1 approaches infinity as t approaches 0 while f2 approaches zero, and that the difference between the two functions decreases as x and y increase.
- A later reply proposes that the integrals can be broken down into intervals, suggesting that each integral approaches zero as x and y go to infinity, though the speed of convergence is not addressed.
- There is a discussion about the nature of the convergence of the integrals and whether the relative difference between them also approaches zero.
- One participant expresses interest in approximating the integrand function under specific limits, noting that symbolic integration of one of the functions is not feasible.
- Another participant introduces the concept of L_p approximation, suggesting that the mean-power approximation could be relevant in this context.
Areas of Agreement / Disagreement
Participants express differing views on the convergence of the integrals and the nature of the approximation. There is no consensus on whether the integrals converge or how closely the functions approximate each other as x and y increase.
Contextual Notes
Some participants note limitations in their ability to express mathematical formulas correctly, which may affect the clarity of the discussion. Additionally, the discussion includes unresolved mathematical steps and assumptions regarding the behavior of the functions involved.