Aquarium on a train during braking

[ChessEnthusiast]

Homework Statement

On a train, there is a passenger who has an aquarium, filled with water.
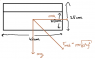
The aquarium's size: 40cm x 25cm x 25cm, and is filled with water up to the height of 20cm (5 cm remaining)

What is the maximal deceleration of the train, such as the entire volume of water will remain in the aquarium?
Assume, that the aquarium is positioned parallel to the direction the train moves.2. The attempt at a solution
(look at the attached image)
I made a sketch and calculated the net force acting on a particle of water.
I also attempted to calculate the mass of water in aquarium (Assumption: 1 liter of water weighs 1 kg)
m = 0.40 * 0.25 * 0.20 = 0.02 kg


I tried using definition of Work:
$$Fx\cos{\theta} = m_{2}gh$$
But I got a crazy answer.

Any suggestions would be strongly appreciated.
Thank you in advance.

 

[BvU]

But I got a crazy answer.

Don't say such things. Show your working.

calculated the net force acting on a particle of water

Nice idea, but you only look at the magnitude. Why ? What does that magnitude tell you about the surface being horizontal when the train stands still ?

I tried using definition of Work

Again: why ? Would it tell you the aquarium does not overflow when the train stands still ?
Anyway: This has little to do with work; can you understand why ?

I also attempted to calculate the mass of water in aquarium

Again ... why ? Would it be different if it were oil, or mercury ?

Please note I'm not trying to be sarcastic, just trying to get you away from all kinds of stray paths.

So now the assistance you asked for (the suggestion )
Ask yourself: what would the angle be if the train braked with an acceleration g ?

 

[ChessEnthusiast]

$$cos{\theta} = \frac{am}{F_{net}}$$
And so, if the acceleration were to be g, then
$$\cos{\theta} = \frac{1}{\sqrt{2}}$$
$$|\theta| = 45$$ degrees

But since we only have 5 centimeters remaining, then the maximal angle we may obtain:
$$\tan{\alpha} = 5 / 40 = 0.125$$
$$\alpha = 7$$ degrees

Is my reasoning all right?

 

[gneill]

Draw the tank and water when the braking acceleration is maximal. Hint: remember that the volume of water must be conserved!

 

[ChessEnthusiast]

These are the two sketches I have created.
Now, my question is:
How could I write beta in terms of theta?
Aren't these angles congruent?

 

[gneill]

Presumably your diagram depicts a train moving to the left but slowing down. The acceleration of the train is thus directed to the right. But the water rushes towards the left side of the tank in the direction of the train's motion. What makes the water move is its inertia, trying to keep moving in the same direction at constant velocity while the train slows down. As such, in the train's frame of reference (which is not an inertial frame because it's accelerating), inertia results in a frame-dependent force (pseudo force) that pushes to the left, not the right.

You'd do better to consider a particle on the surface of the water. If the train acceleration is constant over time and the water is no longer flowing (achieves static conditions) what can you say about the direction of any net force (or better, net acceleration vector) on that particle? Can there be any acceleration along the direction of the surface? Big hint: How does a pond's surface relate to the direction of gravitational acceleration?

 

[ChessEnthusiast]

I have a feeling that the net acceleration you are referring has its direction along the water surface, that is why the surface bends at some angle.

My question is, where does this direction come from, since the force of inertia acts at a 0 degree angle, and the force of gravity is perpendicular to this force.

Another question: Can we assume that the water is in "mechanical equilibrium", and we can consider only horizontal forces?

 

[gneill]

I have a feeling that the net acceleration you are referring has its direction along the water surface, that is why the surface bends at some angle.

No, quite the opposite. If a particle of water at the surface felt an acceleration along the surface (or any component of the acceleration was along the surface) then that particle would want to move along the surface. Since the surface is static, there cannot be a component of the (net) acceleration along the surface. What's does that leave?

My question is, where does this direction come from, since the force of inertia acts at a 0 degree angle, and the force of gravity is perpendicular to this force.

What direction can their sum take? It's the net acceleration that counts.

Another question: Can we assume that the water is in "mechanical equilibrium", and we can consider only horizontal forces?

We can consider the water is in static equilibrium. The net force is not horizontal. Again, what's the direction of the net acceleration and force at a pond's surface? In other words, how do we define "down"?

 

[ChessEnthusiast]

Again, what's the direction of the net acceleration and force at a pond's surface? In other words, how do we define "down"?

Down - direction perpendicular to the water's surface

 

[gneill]

Down - direction perpendicular to the water's surface

Right. So what direction do you infer the net acceleration should be for the aquarium's water surface if it's also in static equilibrium? In other words, what the direction of "down" in the train's frame of reference.

 

[ChessEnthusiast]

It must be this red vector's direction

Now, I think there might be some congruence between these angles.

 

[gneill]

It must be this red vector's direction

Now, I think there might be some congruence between these angles.

Yes indeed. Because the net acceleration must be perpendicular to the water's surface, the angles must be congruent.

Here's my version of your diagram:

 

[ChessEnthusiast]

Thank you very much, that solves the problem as long as Physics is concerned.

However, could you please explain, which vectors are responsible for the congruence of these two angles?

 

[gneill]

Thank you very much, that solves the problem as long as Physics is concerned.

However, could you please explain, which vectors are responsible for the congruence of these two angles?

Imagine the train before braking begins. The local "down" is the same as the inertial track frame's "down" (i.e., vertical). Now imagine that the acceleration due to braking starts gradually. The surface of the water begins to "tip". The perpendicular to the surface must tip through the same angle that the surface does. So the angle of "down" with respect to gravity's direction moves through the same as the angle that the water's surface does with horizontal.

Now, what vector components comprise this "down" direction?" One is gravitational acceleration which remains unchanged and vertical. The other is the inertial "reflection" of the train's horizontal acceleration. i.e., $-a_{train}$. In the non-inertial frame of reference of the train inertia manifests an acceleration that is equal and opposite the train's acceleration. The moving mass "wants" to oppose the change in velocity that the frame of reference is making. We ascribe a force or acceleration to this tendency. To a person on the train, unless he looks out the window to see what's happening it's indistinguishable from a new new gravitational acceleration being superimposed on the usual one. Hence the new "down" direction.