Arc diameter as a function of arc length and chord length

[Robin64]

TL;DR

I'm trying to come up with a formula that defines a bike tire's diameter as a function of interior rim width and tire carcass width

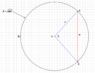
I'm trying to determine if a certain bicycle tire size will fit my bike, and that determination is based on the inflated diameter (or width) of the tire. As such, I'm trying to come up with a formula that will give me the diameter of a bicycle tire as a function of the tire's carcass width and the interior width of the rim. In the attached drawing, w is the interior rim width and S is the width of the tire carcass and the length of the arc ABC. I'm trying to derive the formula as a function of the only two knowns: w and S. Here's my derivation so far:
w=2r*sin(θ/2)
θ=2*arcsin[w/(2r)]
α=2π-θ=2π-2*arcsin[w/(2r)]

r=S/α

r=S/{2π-2*arcsin[w/(2r)]}

I can't see how to eliminate r.

 

[hutchphd]

Look up Sagitta Theorem

 

[Robin64]

That's just seems to introduce another unknown. I don't know the Sagitta length.

 

[hutchphd]

I can't see how to eliminate r.
[/QUOTE]
Looks like you do end up with a transcendental equation for r. My bad.
But you do have a solution albeit a numerical (or graphical) one.

 

[Robin64]

Ok. I suspected that might the case. I can work with a graphical solution.

Thanks.