carlosbgois
- 66
- 0
I've been trying to figure out the most straightforward way of doing this for a while, and would like to get some advice on new approaches, as the one I was using didn't work out at all. So here it is:
The stadium billiard is defined as two semicircles joined by two tangent lines, as shown in the figure attached. Given the angle of a point in the boundary, my goal is to determine the arc length of the boundary, from theta=0 to the collision angle. To do that, I have the parameters of the length of the tangent lines, and the radius of the semicircles (figure.) What approach would fit best here?
Thank you all for your time.
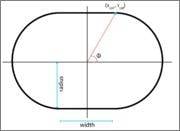
The stadium billiard is defined as two semicircles joined by two tangent lines, as shown in the figure attached. Given the angle of a point in the boundary, my goal is to determine the arc length of the boundary, from theta=0 to the collision angle. To do that, I have the parameters of the length of the tangent lines, and the radius of the semicircles (figure.) What approach would fit best here?
Thank you all for your time.