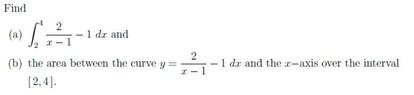Area between the curve and x axis

[TheFallen018]

Hey guys,

I've got this question in my book, and I think that I may be misunderstanding the concept. The book is somewhat lacking on this particular question, and has left me in the dark to some degree.

The question is

Find the area between the curve y=2/(x-1)dx and the x-axis over the interval [2,4].

I was thinking that this should just be the definite integral of the function between [2,4], (ln(9)-2) That being but apparently that is the wrong answer.

Therefore I am left to conclude that I have not understood the question correctly.

If anyone would be able to help clear that up, I would be very grateful.

Kind regards,

TheFallen018

 

[Greg]

$$2\int_2^4\frac{1}{x-1}\,dx=2\ln(3)-2\ln(1)=2\ln(3)$$

 

[TheFallen018]

Oops, I just had a look, and I posted this incorrectly. My function was missing something. What I should have posted was this

Find the area between the curve of y=(2/(x-1))-1, and the x-axis over the interval [2,4]

As far as I can figure, I did have the answer correct, but apparently I was missing a little trick to it.

I'll post a screenshot of the problem, just to clear things up.

View attachment 7618

So, the answer to part a should be ln(9)-2, however, part b seems to be asking just about the same thing as part a, so I'm probably missing something there.

If you'd be able to take another look, that would be really appreciated.

Sorry for the mistake in my previous post.

 

[S.G. Janssens]

Hint: Note (by making a sketch or plot) that the curve given by $y = \frac{2}{x - 1} - 1$ is partly above and partly below the $x$-axis on $[2,4]$. The definite integral gives you the signed area. Where does the curve cross the $x$-axis?

Side remarks: $\ln{9} = \ln{3^2} = 2\ln{3}$. Moreover, it is a bit odd to write the differential $dx$ in the description of the curve (the integrand) itself. It only has meaning when the integrand appears already in the integral.

 

[TheFallen018]

Hint: Note (by making a sketch or plot) that the curve given by $y = \frac{2}{x - 1} - 1$ is partly above and partly below the $x$-axis on $[2,4]$. The definite integral gives you the signed area. Where does the curve cross the $x$-axis?

Side remarks: $\ln{9} = \ln{3^2} = 2\ln{3}$. Moreover, it is a bit odd to write the differential $dx$ in the description of the curve (the integrand) itself. It only has meaning when the integrand appears already in the integral.

I'm not sure if I know what you're getting at. It's clear that part of the curve is above the x axis, and part below. That point of y=0 is obviously at x=3. Perhaps your meaning has escaped me.

As for side remarks, I'm not aware of what your first statement refers to. As for the second, I agree. I also thought it strange that there is a dx after the description of the curve. I assumed that a mistake had been made on the part of whoever wrote up the question sheet.

 

[MarkFL]

I'm not sure if I know what you're getting at. It's clear that part of the curve is above the x axis, and part below. That point of y=0 is obviously at x=3. Perhaps your meaning has escaped me.

As for side remarks, I'm not aware of what your first statement refers to. As for the second, I agree. I also thought it strange that there is a dx after the description of the curve. I assumed that a mistake had been made on the part of whoever wrote up the question sheet.

For part b), you want the area which is a bit different from the definite integral. The definite integral $I$ of the difference between two functions is:

$$I=\int_a^b f(x)-g(x)\,dx=-\int_a^b g(x)-f(x)\,dx$$

The area $A$ between those curves on the same interval is:

$$A=\int_a^b \left|f(x)-g(x)\right|\,dx=\int_a^b \left|g(x)-f(x)\right|\,dx$$

 

[S.G. Janssens]

I'm not sure if I know what you're getting at. It's clear that part of the curve is above the x axis, and part below. That point of y=0 is obviously at x=3. Perhaps your meaning has escaped me.

As for side remarks, I'm not aware of what your first statement refers to. As for the second, I agree. I also thought it strange that there is a dx after the description of the curve. I assumed that a mistake had been made on the part of whoever wrote up the question sheet.

MarkFL already commented on the first part (Yes) Indeed, by "signed area" it is meant that the area corresponding to part of the curve under the $x$-axis is measured with a minus-sign in front.

My first statement was to make sure that it is understood that $\ln{9} = 2\ln{3}$, so the equivalence between post #2 and your own computation of that integral would be clear as well. I'm sorry if this was already clear, but I preferred to err on the side clarification.

 

[TheFallen018]

For part b), you want the area which is a bit different from the definite integral. The definite integral $I$ of the difference between two functions is:

$$I=\int_a^b f(x)-g(x)\,dx=-\int_a^b g(x)-f(x)\,dx$$

The area $A$ between those curves on the same interval is:

$$A=\int_a^b \left|f(x)-g(x)\right|\,dx=\int_a^b \left|g(x)-f(x)\right|\,dx$$

Thanks Mark, I think that's really cleared some things up for me.

If you'd also be so kind, I believe that using the formula you have pointed out, my answer should be

$2\ln{4} -\ln{9}$

Does that sound correct to you?

Thanks again

 

[MarkFL]

Thanks Mark, I think that's really cleared some things up for me.

If you'd also be so kind, I believe that using the formula you have pointed out, my answer should be

$2\ln{4} -\ln{9}$

Does that sound correct to you?

Thanks again

Yes that's correct:

W|A - area between x-axis and y=2/(x-1)-1 on [2,4]

Note: W|A returns a result in a different form, but is recognizable as equivalent to your result.

I would further simplify:

$$A=2\ln(4)-\ln(9)=2\left(\ln(4)-\ln(3)\right)=2\ln\left(\frac{4}{3}\right)$$