Area of lune (Geometry problem)

[Nebuchadnezza]

Here is an interesting brainteaser I found. Looking at the earlier post with the circle and the tangent, I thought people here might be interested. I do have the answer to this riddle so this is not homework by any means.

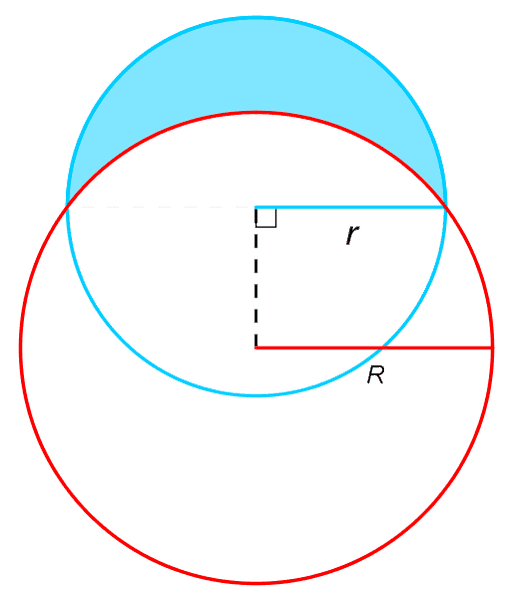
The problem goes as follows

1) Find the area of the crescent-shaped region (called a lune)
bounded by arcs of circles with radii r and R.

2) What is the maximum area of the lune ?

 

[Dschumanji]

For this problem I am assuming the following:

1) The radius of the red circle is fixed and the radius of the blue circle can vary
2) 0 <= r <= R
3) The blue and red circle are always placed such that the diameter of the blue circle is some chord of the red circle

With these three assumptions, the area of the lune must be half of the area of the blue circle minus the area of the circular segment formed by the diameter of the blue circle treated as a chord of the red circle. With a little bit of magic I get the following formula for the area of the lune in terms of the radius of the blue circle:
A(r) = \frac{r^2\pi}{2}+r\sqrt{R^2-r^2}-R^2Sin^{-1}(\frac{r}{R})
Finding the maximum area of the lune requires some calculus. The expression I get is really messy and am too lazy to solve for r explicitly.